KullbackLeiblerCrossEntropy¶

class odl.solvers.functional.default_functionals.KullbackLeiblerCrossEntropy(*args, **kwargs)[source]¶

Bases: Functional

The Kullback-Leibler Cross Entropy divergence functional.

See also

KullbackLeibler: related functional
KullbackLeiblerCrossEntropyConvexConj: the convex conjugate functional

Notes

The functional 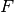$F$ with prior 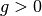$g>0$ is given by: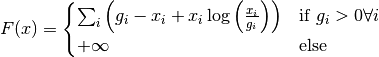

$F(x) = \begin{cases} \sum_{i} \left( g_i - x_i + x_i \log \left( \frac{x_i}{g_i} \right) \right) & \text{if } g_i > 0 \forall i \\ +\infty & \text{else} \end{cases}$

For further information about the functional, see the Wikipedia article on the Kullback Leibler divergence, or read for example this article.

The KL cross entropy functional 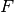$F$ , described above, is related to another functional which is also know as KL divergence. This functional is often used as data discrepancy term in inverse problems, when data is corrupted with Poisson noise. It is obtained by changing place of the prior and the variable. See the See Also section.

For a theoretical exposition, see Csiszar1991.

References

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: The convex conjugate functional of the KL-functional.
domain: Set of objects on which this operator can be evaluated.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: Gradient operator of the functional.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
prior: The prior in the Kullback-Leibler functional.
proximal: Return the proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(space, prior=None)[source]¶

Initialize a new instance.

Parameters:

spaceDiscretizedSpace or TensorSpace: Domain of the functional.
priorspace element-like, optional: Depending on the context, the prior, target or data distribution. It is assumed to be nonnegative. Default: if None it is take as the one-element.