DiscretizedSpace

class odl.discr.discr_space.DiscretizedSpace(partition, tspace, **kwargs)

Bases: TensorSpace

Discretization of a Lebesgue 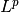space.

Attributes:

axis_labels

Labels for axes when displaying space elements.

byaxis_in

Object to index along input (domain) dimensions.

cell_sides

Side lengths of a cell in an underlying uniform partition.

cell_volume

Cell volume of an underlying uniform partition.

complex_dtype

The complex dtype corresponding to this space's dtype.

complex_space

The space corresponding to this space's complex_dtype.

default_order

Default storage order for new elements in this space.

domain

Set on which functions are defined before discretization.

dtype

Scalar data type of each entry in an element of this space.

element_type

DiscretizedSpaceElement

examples

Return example random vectors.

exponent

Exponent of this space, the p in L^p.

field

Scalar field of numbers for this vector space.

grid

Sampling grid of the discretization mappings.

impl

Name of the implementation back-end.

is_complex

True if this is a space of complex tensors.

is_real

True if this is a space of real tensors.

is_uniform

True if partition is uniform.

is_uniform_byaxis

Boolean tuple showing uniformity of self.partition per axis.

is_uniformly_weighted

True if the weighting is the same for all space points.

is_weighted

True if the tspace is weighted.

itemsize

Size in bytes of one entry in an element of this space.

max_pt

Vector of maximal coordinates of the function domain.

meshgrid

All sampling points in the partition as a sparse meshgrid.

min_pt

Vector of minimal coordinates of the function domain.

nbytes

Total number of bytes in memory used by an element of this space.

ndim

Number of dimensions (= number of axes).

partition

RectPartition of the function domain.

real_dtype

The real dtype corresponding to this space's dtype.

real_space

The space corresponding to this space's real_dtype.

shape

Shape of the underlying partition.

size

Total number of underlying partition cells.

tangent_bundle

The tangent bundle associated with domain using partition.

tspace

Space for the coefficients of the elements of this space.

tspace_type

Tensor space type of this space.

weighting

This space's weighting scheme.

Methods

astype(dtype)	Return a copy of this space with new dtype.
available_dtypes()	Available data types for new elements in this space.
contains_all(other)	Test if all elements in other are contained in this set.
contains_set(other)	Test if other is a subset of this set.
default_dtype([field])	Default data type for new elements in this space.
dist(x1, x2)	Return the distance between x1 and x2.
divide(x1, x2[, out])	Return the pointwise quotient of x1 and x2
element([inp, order])	Create an element from inp or from scratch.
inner(x1, x2)	Return the inner product of x1 and x2.
lincomb(a, x1[, b, x2, out])	Implement out[:] = a * x1 + b * x2.
multiply(x1, x2[, out])	Return the pointwise product of x1 and x2.
norm(x)	Return the norm of x.
one()	Return the element of all ones.
points([order])	All sampling points in the partition.
zero()	Return the element of all zeros.

__init__(partition, tspace, **kwargs)

Initialize a new instance.

Parameters:

partitionRectPartition

Partition of a rectangular spatial domain.

tspaceTensorSpace

Space of elements used for data storage. It must have the same TensorSpace.shape as partition.

axis_labelssequence of str, optional

Names of the axes to use for plotting etc. Default:

• 1D: ['$x$']

• 2D: ['$x$', '$y$']

• 3D: ['$x$', '$y$', '$z$']

• nD: ['$x_1$', '$x_2$', ..., '$x_n$']

Note: The $ signs ensure rendering as LaTeX.