uniform_discr¶

odl.discr.discr_space.uniform_discr(min_pt, max_pt, shape, dtype=None, impl='numpy', **kwargs)[source]¶

Return a uniformly discretized L^p function space.

Parameters:

min_pt, max_ptfloat or sequence of floats: Minimum/maximum corners of the desired function domain.
shapeint or sequence of ints: Number of samples per axis.
dtypeoptional: Data type for the discretized space, must be understood by the numpy.dtype constructor. The default for None depends on the impl backend, usually it is 'float64' or 'float32'.
implstring, optional: Implementation of the data storage arrays.

Returns:

discrDiscretizedSpace: The uniformly discretized function space

Other Parameters:

exponentpositive float, optional

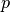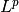The parameter $p$ in $L^p$ . If the exponent is not equal to the default 2.0, the space has no inner product.

nodes_on_bdrybool or sequence, optional

If a sequence is provided, it determines per axis whether to place the last grid point on the boundary (True) or shift it by half a cell size into the interior (False). In each axis, an entry may consist in a single bool or a 2-tuple of bool. In the latter case, the first tuple entry decides for the left, the second for the right boundary. The length of the sequence must be len(shape). A single boolean is interpreted as a global choice for all boundaries. Default: False.

weightingoptional

Use weighted inner product, norm, and dist. The following types are supported as weighting:

None: Use the cell volume as weighting constant (default).
float: Weighting by a constant.
array-like: Point-wise weighting by an array.
Weighting: Use weighting class as-is. Compatibility with this space's elements is not checked during init.

See also

uniform_discr_frompartition: uniform Lp discretization using a given uniform partition of a function domain
uniform_discr_fromspace: uniform discretization from an existing function space
uniform_discr_fromintv: uniform discretization from an existing interval product

Examples

Create real space:

>>> space = uniform_discr([0, 0], [1, 1], (10, 10))
>>> space
uniform_discr([ 0.,  0.], [ 1.,  1.], (10, 10))
>>> space.cell_sides
array([ 0.1,  0.1])
>>> space.dtype
dtype('float64')
>>> space.is_real
True

Create complex space by giving a dtype:

>>> space = uniform_discr([0, 0], [1, 1], (10, 10), dtype=complex)
>>> space
uniform_discr([ 0.,  0.], [ 1.,  1.], (10, 10), dtype=complex)
>>> space.is_complex
True
>>> space.real_space  # Get real counterpart
uniform_discr([ 0.,  0.], [ 1.,  1.], (10, 10))