Functional

class odl.solvers.functional.functional.Functional(*args, **kwargs)

Bases: Operator

Implementation of a functional class.

A functional is an operator f that maps from some domain X to the field of scalars F associated with the domain:

f : X -> F.

Notes

The implementation of the functional class assumes that the domain 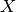is a Hilbert space and that the field of scalars 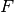is a is the real numbers. It is possible to create functions that do not fulfil these assumptions, however some mathematical results might not be valid in this case. For more information, see the ODL functional guide.

Attributes:

adjoint

Adjoint of this operator (abstract).

convex_conj

Convex conjugate functional of the functional.

domain

Set of objects on which this operator can be evaluated.

grad_lipschitz

Lipschitz constant for the gradient of the functional.

gradient

Gradient operator of the functional.

inverse

Return the operator inverse.

is_functional

True if this operator's range is a Field.

is_linear

True if this operator is linear.

proximal

Proximal factory of the functional.

range

Set in which the result of an evaluation of this operator lies.

Methods

__call__(x[, out])	Return self(x[, out, **kwargs]).
bregman(point, subgrad)	Return the Bregman distance functional.
derivative(point)	Return the derivative operator in the given point.
norm([estimate])	Return the operator norm of this operator.
translated(shift)	Return a translation of the functional.

__init__(space, linear=False, grad_lipschitz=nan)

Initialize a new instance.

Parameters:

spaceLinearSpace

The domain of this functional, i.e., the set of elements to which this functional can be applied.

linearbool, optional

If True, the functional is considered as linear.

grad_lipschitzfloat, optional

The Lipschitz constant of the gradient. Default: nan