IndicatorSimplex

class odl.solvers.functional.default_functionals.IndicatorSimplex(*args, **kwargs)

Bases: Functional

Indicator functional of simplex.

Notes

The functional 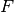is given by: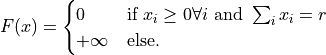

where is the diameter.

Attributes:

adjoint

Adjoint of this operator (abstract).

convex_conj

The convex conjugate.

domain

Set of objects on which this operator can be evaluated.

grad_lipschitz

Lipschitz constant for the gradient of the functional.

gradient

Gradient operator of the functional.

inverse

Return the operator inverse.

is_functional

True if this operator's range is a Field.

is_linear

True if this operator is linear.

proximal

Return the proximal factory of the functional.

range

Set in which the result of an evaluation of this operator lies.

Methods

__call__(x[, out])	Return self(x[, out, **kwargs]).
bregman(point, subgrad)	Return the Bregman distance functional.
derivative(point)	Return the derivative operator in the given point.
norm([estimate])	Return the operator norm of this operator.
translated(shift)	Return a translation of the functional.

__init__(space, diameter=1, sum_rtol=None)

Initialize a new instance.

Parameters:

spaceDiscretizedSpace or TensorSpace

Domain of the functional.

diameterpositive float, optional

Diameter of the simplex.

sum_rtolfloat, optional

Relative tolerance for sum comparison. Default:

• space.dtype == 'float64': 1e-10 * space.size

• Otherwise: 1e-6 * space.size

Examples

Example where a point lies outside the unit simplex ...

>>> space = odl.rn(3)
>>> ind_simplex = IndicatorSimplex(space)
>>> x = space.one()
>>> ind_simplex(x)
inf

... and one where it lies inside the unit simplex.

>>> x /= x.ufuncs.sum()
>>> ind_simplex(x)
0