IndicatorNuclearNormUnitBall¶
- class odl.solvers.functional.default_functionals.IndicatorNuclearNormUnitBall(*args, **kwargs)[source]¶
Bases:
FunctionalIndicator on unit ball of nuclear norm for matrix valued functions.
Notes
For a matrix-valued function
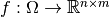 ,
the nuclear norm with parameters
,
the nuclear norm with parameters 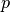 and
and 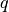 is defined by
is defined by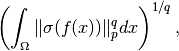
where
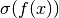 is the vector of singular values of the matrix
is the vector of singular values of the matrix
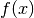 and
and 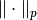 is the usual
is the usual 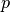 -norm on
-norm on
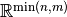 .
.This function is defined as the indicator on the unit ball of the nuclear norm, that is, 0 if the nuclear norm is less than 1, and infinity else.
For a detailed description of its properties, e.g, its proximal, convex conjugate and more, see [Du+2016].
References
[Du+2016] J. Duran, M. Moeller, C. Sbert, and D. Cremers. Collaborative Total Variation: A General Framework for Vectorial TV Models SIAM Journal of Imaging Sciences 9(1): 116--151, 2016.
- Attributes:
adjointAdjoint of this operator (abstract).
convex_conjConvex conjugate of the unit ball indicator of the nuclear norm.
domainSet of objects on which this operator can be evaluated.
grad_lipschitzLipschitz constant for the gradient of the functional.
gradientGradient operator of the functional.
inverseReturn the operator inverse.
is_functionalTrueif this operator's range is aField.is_linearTrueif this operator is linear.proximalThe proximal operator.
rangeSet in which the result of an evaluation of this operator lies.
Methods
__call__(x[, out])Return
self(x[, out, **kwargs]).bregman(point, subgrad)Return the Bregman distance functional.
derivative(point)Return the derivative operator in the given point.
norm([estimate])Return the operator norm of this operator.
translated(shift)Return a translation of the functional.
- __init__(space, outer_exp=1, singular_vector_exp=2)[source]¶
Initialize a new instance.
- Parameters:
- space
ProductSpaceofProductSpaceofTensorSpace Domain of the functional.
- outer_exp{1, 2, inf}, optional
Exponent for the outer norm.
- singular_vector_exp{1, 2, inf}, optional
Exponent for the norm for the singular vectors.
- space
Examples
Simple example, nuclear norm of matrix valued function with all ones in 3 points. The singular values are [2, 0], which has squared 2-norm 2. Since there are 3 points, the expected total value is 6. Since the nuclear norm is larger than 1, the indicator is infinity.
>>> r3 = odl.rn(3) >>> space = odl.ProductSpace(odl.ProductSpace(r3, 2), 2) >>> norm = IndicatorNuclearNormUnitBall(space) >>> norm(space.one()) inf