ProductSpace¶

class odl.space.pspace.ProductSpace(*spaces, **kwargs)[source]¶

Bases: LinearSpace

Cartesian product of LinearSpace's.

A product space is the Cartesian product X_1 x ... x X_n of linear spaces X_i. It is itself a linear space, where the linear combination is defined component-wise. Inner product, norm and distance can also be defined in natural ways from the corresponding functions in the individual components.

Attributes:

complex_space: Variant of this space with complex dtype.
dtype: The data type of this space.
element_type: ProductSpaceElement
examples: Return examples from all sub-spaces.
exponent: Exponent of the product space norm/dist, None for custom.
field: Scalar field of numbers for this vector space.
is_complex: True if this is a space of complex valued vectors.
is_power_space: True if all member spaces are equal.
is_real: True if this is a space of real valued vectors.
is_weighted: Return True if the space is not weighted by constant 1.0.
nbytes: Total number of bytes in memory used by an element of this space.
real_space: Variant of this space with real dtype.
shape: Total spaces per axis, computed recursively.
size: Total number of involved spaces, computed recursively.
spaces: A tuple containing all spaces.
weighting: This space's weighting scheme.

Methods

`astype`(dtype)	Return a copy of this space with new `dtype`.
`contains_all`(other)	Test if all elements in `other` are contained in this set.
`contains_set`(other)	Test if `other` is a subset of this set.
`dist`(x1, x2)	Return the distance between `x1` and `x2`.
`divide`(x1, x2[, out])	Return the pointwise quotient of `x1` and `x2`
`element`([inp, cast])	Create an element in the product space.
`inner`(x1, x2)	Return the inner product of `x1` and `x2`.
`lincomb`(a, x1[, b, x2, out])	Implement `out[:] = a * x1 + b * x2`.
`multiply`(x1, x2[, out])	Return the pointwise product of `x1` and `x2`.
`norm`(x)	Return the norm of `x`.
`one`()	Create the one element of the product space.
`zero`()	Create the zero element of the product space.

__init__(*spaces, **kwargs)[source]¶

Initialize a new instance.

Parameters:

space1,...,spaceNLinearSpace or int

The individual spaces ("factors / parts") in the product space. Can also be given as space, n with n integer, in which case the power space space ** n is created.

exponentnon-zero float or float('inf'), optional

Order of the product distance/norm, i.e.

dist(x, y) = np.linalg.norm(x-y, ord=exponent)

norm(x) = np.linalg.norm(x, ord=exponent)

Values 0 <= exponent < 1 are currently unsupported due to numerical instability. See Notes for further information about the interpretation of the values.

Default: 2.0

fieldField, optional

Scalar field of the resulting space. Default: spaces[0].field

weightingoptional

Use weighted inner product, norm, and dist. The following types are supported as weighting:

None : no weighting (default)

Weighting : weighting class, used directly. Such a class instance can be retrieved from the space by the ProductSpace.weighting property.

array-like : weigh each component with one entry from the array. The array must be one-dimensional and have the same length as the number of spaces.

float : same weighting factor in each component

Other Parameters:

distcallable, optional

The distance function defining a metric on the space. It must accept two ProductSpaceElement arguments and fulfill the following mathematical conditions for any three space elements x, y, z:

dist(x, y) >= 0
dist(x, y) = 0 if and only if x = y
dist(x, y) = dist(y, x)
dist(x, y) <= dist(x, z) + dist(z, y)

By default, dist(x, y) is calculated as norm(x - y).

Cannot be combined with: weighting, norm, inner

normcallable, optional

The norm implementation. It must accept an ProductSpaceElement argument, return a float and satisfy the following conditions for all space elements x, y and scalars s:

||x|| >= 0
||x|| = 0 if and only if x = 0
||s * x|| = |s| * ||x||
||x + y|| <= ||x|| + ||y||

By default, norm(x) is calculated as inner(x, x).

Cannot be combined with: weighting, dist, inner

innercallable, optional

The inner product implementation. It must accept two ProductSpaceElement arguments, return a element from the field of the space (real or complex number) and satisfy the following conditions for all space elements x, y, z and scalars s:

<x, y> = conj(<y, x>)
<s*x + y, z> = s * <x, z> + <y, z>
<x, x> = 0 if and only if x = 0

Cannot be combined with: weighting, dist, norm

See also

ProductSpaceArrayWeighting
ProductSpaceConstWeighting

Notes

Inner product, norm and distance are evaluated by collecting the result of the corresponding operation in the individual components and reducing the resulting vector to a single number. The exponent parameter influences only this last part, not the computations in the individual components. We give the exact definitions in the following:

Let 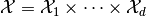$\mathcal{X} = \mathcal{X}_1 \times \dots \times \mathcal{X}_d$ be a product space, and 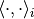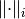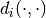$\langle \cdot, \cdot\rangle_i$ , $\lVert \cdot \rVert_i$ , $d_i(\cdot, \cdot)$ be inner products, norms and distances in the respective component spaces.

Inner product:

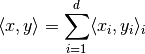
$\langle x, y \rangle = \sum_{i=1}^d \langle x_i, y_i \rangle_i$

Norm:

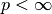$p < \infty$ :

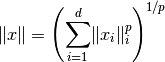
$\lVert x\rVert = \left( \sum_{i=1}^d \lVert x_i \rVert_i^p \right)^{1/p}$

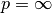$p = \infty$ :

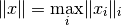
$\lVert x\rVert = \max_i \lVert x_i \rVert_i$

Distance:

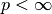$p < \infty$ :

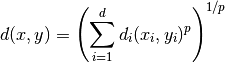
$d(x, y) = \left( \sum_{i=1}^d d_i(x_i, y_i)^p \right)^{1/p}$

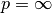$p = \infty$ :

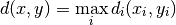
$d(x, y) = \max_i d_i(x_i, y_i)$

To implement own versions of these functions, you can use the following snippet to gather the vector of norms (analogously for inner products and distances):

norms = np.fromiter(
    (xi.norm() for xi in x),
    dtype=np.float64, count=len(x))

Examples

Product of two rn spaces

>>> r2x3 = ProductSpace(odl.rn(2), odl.rn(3))

Powerspace of rn space

>>> r2x2x2 = ProductSpace(odl.rn(2), 3)