ProductSpaceArrayWeighting¶

class odl.space.pspace.ProductSpaceArrayWeighting(array, exponent=2.0)[source]¶

Array weighting for ProductSpace.

This class defines a weighting that has a different value for each index defined in a given space. See Notes for mathematical details.

Attributes:

Methods

`dist`(x1, x2)	Calculate the distance between two elements.
`equiv`(other)	Return True if other is an equivalent weighting.
`inner`(x1, x2)	Calculate the array-weighted inner product of two elements.
`is_valid`()	Return True if the array is a valid weight, i.e. positive.
`norm`(x)	Calculate the array-weighted norm of an element.

__init__(array, exponent=2.0)[source]¶

Initialize a new instance.

Parameters:

array1-dim. array-like: Weighting array of the inner product.
exponentpositive float, optional: Exponent of the norm. For values other than 2.0, no inner product is defined.

Notes

For exponent 2.0, a new weighted inner product with array 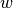$w$ is defined as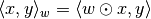

$\langle x, y \rangle_w = \langle w \odot x, y \rangle$

with component-wise multiplication 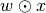$w \odot x$ . For other exponents, only norm and dist are defined. In the case of exponent inf, the weighted norm is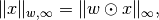

$\|x\|_{w,\infty} = \|w \odot x\|_\infty,$

otherwise it is

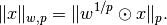
$\|x\|_{w,p} = \|w^{1/p} \odot x\|_p.$
Note that this definition does not fulfill the limit property in 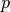$p$ , i.e.,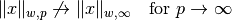

$\|x\|_{w,p} \not\to \|x\|_{w,\infty} \quad\text{for } p \to \infty$

unless 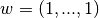$w = (1,...,1)$ . The reason for this choice is that the alternative with the limit property consists in ignoring the weights altogether.
The array may only have positive entries, otherwise it does not define an inner product or norm, respectively. This is not checked during initialization.