IndicatorLpUnitBall¶
- class odl.solvers.functional.default_functionals.IndicatorLpUnitBall(*args, **kwargs)[source]¶
Bases:
FunctionalThe indicator function on the unit ball in given the
Lpnorm.It does not implement
gradientsince it is not differentiable everywhere.Notes
This functional is defined as
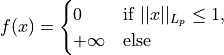
where
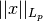 is the
is the 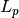 -norm, which for finite values
of
-norm, which for finite values
of 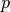 is defined as
is defined as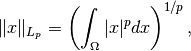
and for
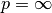 it is defined as
it is defined as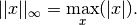
The functional also allows noninteger and nonpositive values of the exponent
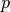 , however in this case
, however in this case 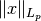 is not a
norm.
is not a
norm.- Attributes:
adjointAdjoint of this operator (abstract).
convex_conjThe conjugate functional of IndicatorLpUnitBall.
domainSet of objects on which this operator can be evaluated.
exponentExponent corresponding to the norm.
grad_lipschitzLipschitz constant for the gradient of the functional.
gradientGradient operator of the functional.
inverseReturn the operator inverse.
is_functionalTrueif this operator's range is aField.is_linearTrueif this operator is linear.proximalReturn the
proximal factoryof the functional.rangeSet in which the result of an evaluation of this operator lies.
Methods
__call__(x[, out])Return
self(x[, out, **kwargs]).bregman(point, subgrad)Return the Bregman distance functional.
derivative(point)Return the derivative operator in the given point.
norm([estimate])Return the operator norm of this operator.
translated(shift)Return a translation of the functional.
- __init__(space, exponent)[source]¶
Initialize a new instance.
- Parameters:
- space
DiscretizedSpaceorTensorSpace Domain of the functional.
- exponentint or infinity
Specifies wich norm to use.
- space