ProductSpaceOperator¶

class odl.operator.pspace_ops.ProductSpaceOperator(*args, **kwargs)[source]¶

Bases: Operator

A "matrix of operators" on product spaces.

For example a matrix of operators can act on a vector by

ProductSpaceOperator([[A, B], [C, D]])([x, y]) = [A(x) + B(y), C(x) + D(y)]

See also

BroadcastOperator: Case when a single argument is used by several ops.
ReductionOperator: Calculates sum of operator results.
DiagonalOperator: Case where the 'matrix' is diagonal.

Notes

This is intended for the case where an operator can be decomposed as a linear combination of "sub-operators", e.g.

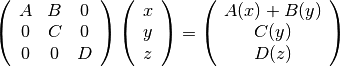
$\left( \begin{array}{ccc} A & B & 0 \\ 0 & C & 0 \\ 0 & 0 & D \end{array}\right) \left( \begin{array}{c} x \\ y \\ z \end{array}\right) = \left( \begin{array}{c} A(x) + B(y) \\ C(y) \\ D(z) \end{array}\right)$

Mathematically, a ProductSpaceOperator is an operator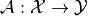

$\mathcal{A}: \mathcal{X} \to \mathcal{Y}$

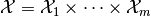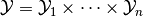between product spaces $\mathcal{X}=\mathcal{X}_1 \times\dots\times \mathcal{X}_m$ and $\mathcal{Y}=\mathcal{Y}_1 \times\dots\times \mathcal{Y}_n$ which can be written in the form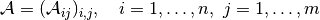

$\mathcal{A} = (\mathcal{A}_{ij})_{i,j}, \quad i = 1, \dots, n, \ j = 1, \dots, m$

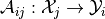with component operators $\mathcal{A}_{ij}: \mathcal{X}_j \to \mathcal{Y}_i$ .

Its action on a vector 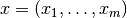$x = (x_1, \dots, x_m)$ is defined as the matrix multiplication

$[\mathcal{A}(x)]_i = \sum_{j=1}^m \mathcal{A}_{ij}(x_j).$

Attributes:

adjoint: Adjoint of this operator.
domain: Set of objects on which this operator can be evaluated.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
ops: The sparse operator matrix representing this operator.
range: Set in which the result of an evaluation of this operator lies.
shape: Shape of the matrix of operators.
size: Total size of the matrix of operators.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`derivative`(x)	Derivative of the product space operator.
`norm`([estimate])	Return the operator norm of this operator.

__init__(operators, domain=None, range=None)[source]¶

Initialize a new instance.

Parameters:

operatorsarray-like: An array of Operator's, must be 2-dimensional.
domainProductSpace, optional: Domain of the operator. If not provided, it is tried to be inferred from the operators. This requires each column to contain at least one operator.
rangeProductSpace, optional: Range of the operator. If not provided, it is tried to be inferred from the operators. This requires each row to contain at least one operator.

Examples

>>> r3 = odl.rn(3)
>>> pspace = odl.ProductSpace(r3, r3)
>>> I = odl.IdentityOperator(r3)
>>> x = pspace.element([[1, 2, 3],
...                     [4, 5, 6]])

Create an operator that sums two inputs:

>>> prod_op = odl.ProductSpaceOperator([[I, I]])
>>> prod_op(x)
ProductSpace(rn(3), 1).element([
    [ 5.,  7.,  9.]
])

Diagonal operator -- 0 or None means ignore, or the implicit zero operator:

>>> prod_op = odl.ProductSpaceOperator([[I, 0],
...                                     [0, I]])
>>> prod_op(x)
ProductSpace(rn(3), 2).element([
    [ 1.,  2.,  3.],
    [ 4.,  5.,  6.]
])

If a column is empty, the operator domain must be specified. The same holds for an empty row and the range of the operator:

>>> prod_op = odl.ProductSpaceOperator([[I, 0],
...                                     [I, 0]], domain=r3 ** 2)
>>> prod_op(x)
ProductSpace(rn(3), 2).element([
    [ 1.,  2.,  3.],
    [ 1.,  2.,  3.]
])
>>> prod_op = odl.ProductSpaceOperator([[I, I],
...                                     [0, 0]], range=r3 ** 2)
>>> prod_op(x)
ProductSpace(rn(3), 2).element([
    [ 5.,  7.,  9.],
    [ 0.,  0.,  0.]
])