ComponentProjection¶

class odl.operator.pspace_ops.ComponentProjection(*args, **kwargs)[source]¶

Bases: Operator

Projection onto the subspace identified by an index.

For a product space 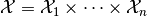$\mathcal{X} = \mathcal{X}_1 \times \dots \times \mathcal{X}_n$ , the component projection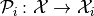

$\mathcal{P}_i: \mathcal{X} \to \mathcal{X}_i$

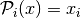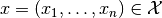is given by $\mathcal{P}_i(x) = x_i$ for an element $x = (x_1, \dots, x_n) \in \mathcal{X}$ .

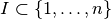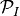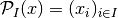More generally, for an index set $I \subset \{1, \dots, n\}$ , the projection operator $\mathcal{P}_I$ is defined by $\mathcal{P}_I(x) = (x_i)_{i \in I}$ .

Note that this is a special case of a product space operator where the "operator matrix" has only one row and contains only identity operators.

Attributes:

adjoint: The adjoint operator.
domain: Set of objects on which this operator can be evaluated.
index: Index of the subspace.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`derivative`(point)	Return the operator derivative at `point`.
`norm`([estimate])	Return the operator norm of this operator.

__init__(space, index)[source]¶

Initialize a new instance.

Parameters:

spaceProductSpace: Space to project from.
indexint, slice, or list: Indices defining the subspace. If index is not an integer, the Operator.range of this operator is also a ProductSpace.

Examples

>>> r1 = odl.rn(1)
>>> r2 = odl.rn(2)
>>> r3 = odl.rn(3)
>>> pspace = odl.ProductSpace(r1, r2, r3)

Projection on n-th component:

>>> proj = odl.ComponentProjection(pspace, 0)
>>> x = [[1],
...      [2, 3],
...      [4, 5, 6]]
>>> proj(x)
rn(1).element([ 1.])

Projection on sub-space:

>>> proj = odl.ComponentProjection(pspace, [0, 2])
>>> proj(x)
ProductSpace(rn(1), rn(3)).element([
    [ 1.],
    [ 4.,  5.,  6.]
])