FunctionalQuotient.bregman¶

FunctionalQuotient.bregman(point, subgrad)¶

Return the Bregman distance functional.

Parameters:

pointelement of functional.domain: Point from which to define the Bregman distance.
subgradelement of functional.domain: A subgradient of functional in point. If it exists, a valid option is functional.gradient(point).

Returns:

outBregmanDistance: The Bregman distance functional.

Notes

Given a functional 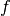$f$ , a point 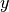$y$ , and a (sub)gradient 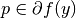$p \in \partial f(y)$ , the Bregman distance functional 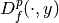$D_f^p(\cdot, y)$ in a point 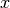$x$ is given by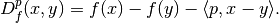

$D_f^p(x, y) = f(x) - f(y) - \langle p, x - y \rangle.$

For mathematical details, see [Bur2016]. See also the Wikipedia article: https://en.wikipedia.org/wiki/Bregman_divergence

References

[Bur2016] Burger, M. Bregman Distances in Inverse Problems and Partial Differential Equation. In: Advances in Mathematical Modeling, Optimization and Optimal Control, 2016. p. 3-33.