BregmanDistance¶

class odl.solvers.functional.functional.BregmanDistance(*args, **kwargs)[source]¶

Bases: Functional

The Bregman distance functional.

The Bregman distance, also refered to as the Bregman divergence, is similar to a metric but satisfies neither the triangle inequality nor symmetry. Nevertheless, the Bregman distance is used in variational regularization of inverse problems, see, e.g., [Bur2016].

Notes

Given a functional 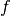$f$ , a point 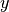$y$ , and a (sub)gradient 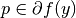$p \in \partial f(y)$ , the Bregman distance functional 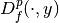$D_f^p(\cdot, y)$ in a point 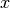$x$ is given by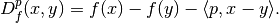

$D_f^p(x, y) = f(x) - f(y) - \langle p, x - y \rangle.$

For mathematical details, see [Bur2016]. See also the Wikipedia article: https://en.wikipedia.org/wiki/Bregman_divergence

References

[Bur2016] Burger, M. Bregman Distances in Inverse Problems and Partial Differential Equation. In: Advances in Mathematical Modeling, Optimization and Optimal Control, 2016. p. 3-33.

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: The convex conjugate
domain: Set of objects on which this operator can be evaluated.
functional: The functional used to define the Bregman distance.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: Gradient operator of the functional.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
point: The point used to define the Bregman distance.
proximal: Return the proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.
subgrad: The subgradient used to define the Bregman distance.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(functional, point, subgrad)[source]¶

Initialize a new instance.

Parameters:

functionalFunctional: Functional on which to base the Bregman distance.
pointelement of functional.domain: Point from which to define the Bregman distance.
subgradelement of functional.domain: A subgradient of functional in point. If it exists, a valid option is functional.gradient(point).

Examples

Example of initializing the Bregman distance functional:

>>> space = odl.uniform_discr(0, 1, 10)
>>> l2_squared = odl.solvers.L2NormSquared(space)
>>> point = space.one()
>>> subgrad = l2_squared.gradient(point)
>>> bregman_dist = odl.solvers.BregmanDistance(
...     l2_squared, point, subgrad)

This is gives squared L2 distance to the given point, ||x - 1||^2:

>>> expected_functional = l2_squared.translated(point)
>>> bregman_dist(space.zero()) == expected_functional(space.zero())
True