SeparableSum¶

class odl.solvers.functional.default_functionals.SeparableSum(*args, **kwargs)[source]¶

Bases: Functional

The functional corresponding to separable sum of functionals.

The separable sum of functionals f_1, f_2, ..., f_n is given by

h(x_1, x_2, ..., x_n) = sum_i^n f_i(x_i)

The separable sum is thus defined for any collection of functionals with the same range.

Notes

The separable sum of functionals 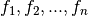$f_1, f_2, ..., f_n$ is given by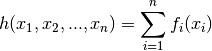

$h(x_1, x_2, ..., x_n) = \sum_{i=1}^n f_i(x_i)$

It has several useful features that also distribute. For example, the gradient is a DiagonalOperator:

$[\nabla h](x_1, x_2, ..., x_n) = [\nabla f_1(x_i), \nabla f_2(x_i), ..., \nabla f_n(x_i)]$

The convex conjugate is also a separable sum:

$[h^*](y_1, y_2, ..., y_n) = \sum_{i=1}^n f_i^*(y_i)$

And the proximal distributes:

$\mathrm{prox}_{\sigma h}(x_1, x_2, ..., x_n) = [\mathrm{prox}_{\sigma f_1}(x_1), \mathrm{prox}_{\sigma f_2}(x_2), ..., \mathrm{prox}_{\sigma f_n}(x_n)].$

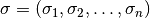If $\sigma = (\sigma_1, \sigma_2, \ldots, \sigma_n)$ is a list of positive float's, then it distributes, too:

$\mathrm{prox}_{\sigma h}(x_1, x_2, ..., x_n) = [\mathrm{prox}_{\sigma_1 f_1}(x_1), \mathrm{prox}_{\sigma_2 f_2}(x_2), ..., \mathrm{prox}_{\sigma_n f_n}(x_n)].$

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: The convex conjugate functional.
domain: Set of objects on which this operator can be evaluated.
functionals: The summands of the functional.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: Gradient operator of the functional.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
proximal: Return the proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(*functionals)[source]¶

Initialize a new instance.

Parameters:

functional1, ..., functionalNFunctional: The functionals in the sum. Can also be given as space, n with n integer, in which case the functional is repeated n times.

Examples

Create functional f([x1, x2]) = ||x1||_1 + ||x2||_2:

>>> space = odl.rn(3)
>>> l1 = odl.solvers.L1Norm(space)
>>> l2 = odl.solvers.L2Norm(space)
>>> f_sum = odl.solvers.SeparableSum(l1, l2)

The proximal factory allows using vector-valued stepsizes:

>>> x = f_sum.domain.one()
>>> f_sum.proximal([0.5, 2.0])(x)
ProductSpace(rn(3), 2).element([
    [ 0.5,  0.5,  0.5],
    [ 0.,  0.,  0.]
])

Create functional f([x1, ... ,xn]) = \sum_i ||xi||_1:

>>> f_sum = odl.solvers.SeparableSum(l1, 5)