MoreauEnvelope¶

class odl.solvers.functional.default_functionals.MoreauEnvelope(*args, **kwargs)[source]¶

Bases: Functional

Moreau envelope of a convex functional.

The Moreau envelope is a way to smooth an arbitrary convex functional such that its gradient can be computed given the proximal of the original functional. The new functional has the same critical points as the original. It is also called the Moreau-Yosida regularization.

Note that the only computable property of the Moreau envelope is the gradient, the functional itself cannot be evaluated efficiently.

See Proximal Algorithms for more information.

Notes

The Moreau envelope of a convex functional 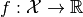$f : \mathcal{X} \rightarrow \mathbb{R}$ multiplied by a scalar 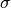$\sigma$ is defined by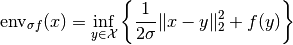

$\mathrm{env}_{\sigma f}(x) = \inf_{y \in \mathcal{X}} \left\{ \frac{1}{2 \sigma} \| x - y \|_2^2 + f(y) \right\}$

The gradient of the envelope is given by

$[\nabla \mathrm{env}_{\sigma f}](x) = \frac{1}{\sigma} (x - \mathrm{prox}_{\sigma f}(x))$

Example: if 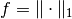$f = \| \cdot \|_1$ , then

$[\mathrm{env}_{\sigma \| \cdot \|_1}(x)]_i = \begin{cases} \frac{1}{2 \sigma} x_i^2 & \text{if } |x_i| \leq \sigma \\ |x_i| - \frac{\sigma}{2} & \text{if } |x_i| > \sigma, \end{cases}$

which is the usual Huber functional.

References

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: Convex conjugate functional of the functional.
domain: Set of objects on which this operator can be evaluated.
functional: The functional that has been regularized.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: The gradient operator.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
proximal: Proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.
sigma: Regularization constant, larger means stronger regularization.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(functional, sigma=1.0)[source]¶

Initialize an instance.

Parameters:

functionalFunctional: The functional f in the definition of the Moreau envelope that is to be smoothed.
sigmapositive float, optional: The scalar sigma in the definition of the Moreau envelope. Larger values mean stronger smoothing.

Examples

Create smoothed l1 norm:

>>> space = odl.rn(3)
>>> l1_norm = odl.solvers.L1Norm(space)
>>> smoothed_l1 = MoreauEnvelope(l1_norm)