L1Norm

class odl.solvers.functional.default_functionals.L1Norm(*args, **kwargs)

Bases: LpNorm

The functional corresponding to L1-norm.

The L1-norm, ||x||_1, is defined as the integral/sum of |x|.

Notes

If the functional is defined on an 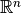-like space, the 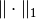-norm is defined as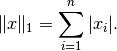

If the functional is defined on an 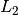-like space, the 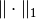-norm is defined as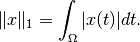

The proximal factory allows using vector-valued stepsizes:

>>> space = odl.rn(3)
>>> f = odl.solvers.L1Norm(space)
>>> x = space.one()
>>> f.proximal([0.5, 1.0, 1.5])(x)
rn(3).element([ 0.5,  0. ,  0. ])

Attributes:

adjoint

Adjoint of this operator (abstract).

convex_conj

The convex conjugate functional of the Lp-norm.

domain

Set of objects on which this operator can be evaluated.

grad_lipschitz

Lipschitz constant for the gradient of the functional.

gradient

Gradient operator of the functional.

inverse

Return the operator inverse.

is_functional

True if this operator's range is a Field.

is_linear

True if this operator is linear.

proximal

Return the proximal factory of the functional.

range

Set in which the result of an evaluation of this operator lies.

Methods

__call__(x[, out])	Return self(x[, out, **kwargs]).
bregman(point, subgrad)	Return the Bregman distance functional.
derivative(point)	Return the derivative operator in the given point.
norm([estimate])	Return the operator norm of this operator.
translated(shift)	Return a translation of the functional.

__init__(space)

Initialize a new instance.

Parameters:

spaceDiscretizedSpace or TensorSpace

Domain of the functional.