Huber¶

class odl.solvers.functional.default_functionals.Huber(*args, **kwargs)[source]¶

Bases: Functional

The Huber functional.

Notes

The Huber norm is the integral over a smoothed norm. In detail, it is given by

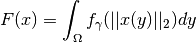
$F(x) = \int_\Omega f_{\gamma}(||x(y)||_2) dy$

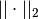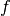where $||\cdot||_2$ denotes the Euclidean norm for vector-valued functions which reduces to the absolute value for scalar-valued functions. The function $f$ with smoothing 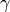$\gamma$ is given by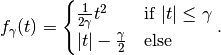

$f_{\gamma}(t) = \begin{cases} \frac{1}{2 \gamma} t^2 & \text{if } |t| \leq \gamma \\ |t| - \frac{\gamma}{2} & \text{else} \end{cases}.$

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: The convex conjugate
domain: Set of objects on which this operator can be evaluated.
gamma: The smoothing parameter of the Huber norm functional.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: Gradient operator of the functional.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
proximal: Return the proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(space, gamma)[source]¶

Initialize a new instance.

Parameters:

spaceTensorSpace: Domain of the functional.
gammafloat: Smoothing parameter of the Huber functional. If gamma = 0, the functional is non-smooth and corresponds to the usual L1 norm. For gamma > 0, it has a 1/gamma-Lipschitz gradient so that its convex conjugate is gamma-strongly convex.

Examples

Example of initializing the Huber functional:

>>> space = odl.uniform_discr(0, 1, 14)
>>> gamma = 0.1
>>> huber_norm = odl.solvers.Huber(space, gamma=0.1)

Check that if all elements are > gamma we get the L1-norm up to a constant:

>>> x = 2 * gamma * space.one()
>>> tol = 1e-5
>>> constant = gamma / 2 * space.one().inner(space.one())
>>> f = odl.solvers.L1Norm(space) - constant
>>> abs(huber_norm(x) - f(x)) < tol
True

Check that if all elements are < gamma we get the squared L2-norm times the weight 1/(2*gamma):

>>> x = gamma / 2 * space.one()
>>> f = 1 / (2 * gamma) * odl.solvers.L2NormSquared(space)
>>> abs(huber_norm(x) - f(x)) < tol
True

Compare Huber- and L1-norm for vanishing smoothing gamma=0:

>>> x = odl.phantom.white_noise(space)
>>> huber_norm = odl.solvers.Huber(space, gamma=0)
>>> l1_norm = odl.solvers.L1Norm(space)
>>> abs(huber_norm(x) - l1_norm(x)) < tol
True

Redo previous example for a product space in two dimensions:

>>> domain = odl.uniform_discr([0, 0], [1, 1], [5, 5])
>>> space = odl.ProductSpace(domain, 2)
>>> x = odl.phantom.white_noise(space)
>>> huber_norm = odl.solvers.Huber(space, gamma=0)
>>> l1_norm = odl.solvers.GroupL1Norm(space, 2)
>>> abs(huber_norm(x) - l1_norm(x)) < tol
True