LinDeformFixedDisp¶
- class odl.deform.linearized.LinDeformFixedDisp(*args, **kwargs)[source]¶
Bases:
OperatorDeformation operator with fixed displacement acting on templates.
The operator has a fixed displacement field
vand maps a templateIto the new functionx --> I(x + v(x)).See also
LinDeformFixedTemplDeformation with a fixed template.
Notes
For
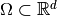 , we take
, we take 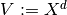 to be the space of displacement fields, where
to be the space of displacement fields, where 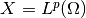 is the template space. Hence the deformation operator with the fixed
displacement field
is the template space. Hence the deformation operator with the fixed
displacement field 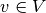 maps
maps 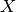 into
into 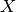 :
: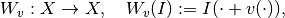
i.e.,
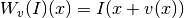 .
.This operator is linear, so its derivative is itself, but it may not be bounded and may thus not have a formal adjoint. For "small"
 ,
though, one can approximate the adjoint by
,
though, one can approximate the adjoint by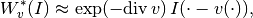
i.e.,
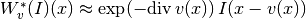 .
.- Attributes:
adjointAdjoint of the linear operator.
displacementFixed displacement field of this deformation operator.
domainSet of objects on which this operator can be evaluated.
interpInterpolation scheme or tuple of per-axis interpolation schemes.
interp_byaxisTuple of per-axis interpolation schemes.
inverseInverse deformation using
-vas displacement.is_functionalTrueif this operator's range is aField.is_linearTrueif this operator is linear.rangeSet in which the result of an evaluation of this operator lies.
Methods
__call__(x[, out])Return
self(x[, out, **kwargs]).derivative(point)Return the operator derivative at
point.norm([estimate])Return the operator norm of this operator.
- __init__(displacement, templ_space=None, interp='linear')[source]¶
Initialize a new instance.
- Parameters:
- displacementelement of a power space of
DiscretizedSpace Fixed displacement field used in the deformation.
- templ_space
DiscretizedSpace, optional Template space on which this operator is applied, i.e. the operator domain and range. It must fulfill
templ_space[0].partition == displacement.space.partition, so this option is useful mainly for support of complex spaces and if different interpolations should be used for displacement and template.Default:
displacement.space[0]- interpstr or sequence of str
Interpolation type that should be used to sample the template on the deformed grid. A single value applies to all axes, and a sequence gives the interpolation scheme per axis.
Supported values:
'nearest','linear'
- displacementelement of a power space of
Examples
Create a simple 1D template to initialize the operator and apply it to a displacement field. Where the displacement is zero, the output value is the same as the input value. In the 4-th point, the value is taken from 0.2 (one cell) to the left, i.e. 1.0.
>>> space = odl.uniform_discr(0, 1, 5) >>> disp_field = space.tangent_bundle.element([[0, 0, 0, -0.2, 0]]) >>> op = odl.deform.LinDeformFixedDisp(disp_field, interp='nearest') >>> template = [0, 0, 1, 0, 0] >>> print(op([0, 0, 1, 0, 0])) [ 0., 0., 1., 1., 0.]
The result depends on the chosen interpolation. With 'linear' interpolation and an offset of half the distance between two points, 0.1, one gets the mean of the values.
>>> disp_field = space.tangent_bundle.element([[0, 0, 0, -0.1, 0]]) >>> op = odl.deform.LinDeformFixedDisp(disp_field, interp='linear') >>> template = [0, 0, 1, 0, 0] >>> print(op(template)) [ 0. , 0. , 1. , 0.5, 0. ]