newtons_method¶

odl.solvers.smooth.newton.newtons_method(f, x, line_search=1.0, maxiter=1000, tol=1e-16, cg_iter=None, callback=None)[source]¶

Newton's method for minimizing a functional.

Parameters:

fFunctional: Goal functional. Needs to have f.gradient and f.gradient.derivative.
xop.domain element: Starting point of the iteration
line_searchfloat or LineSearch, optional: Strategy to choose the step length. If a float is given, uses it as a fixed step length.
maxiterint, optional: Maximum number of iterations.
tolfloat, optional: Tolerance that should be used for terminating the iteration.
cg_iterint, optional: Number of iterations in the the conjugate gradient solver, for computing the search direction.
callbackcallable, optional: Object executing code per iteration, e.g. plotting each iterate

Notes

This is a general and optimized implementation of Newton's method for solving the problem:

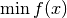
$\min f(x)$

for a differentiable function 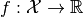$f: \mathcal{X}\to \mathbb{R}$ on a Hilbert space 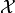$\mathcal{X}$ . It does so by finding a zero of the gradient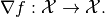

$\nabla f: \mathcal{X} \to \mathcal{X}.$

of finding a root of a function.

The algorithm is well-known and there is a vast literature about it. Among others, the method is described in [BV2004], Sections 9.5 and 10.2 (book available online), [GNS2009], Section 2.7 for solving nonlinear equations and Section 11.3 for its use in minimization, and wikipedia on Newton's_method.

The algorithm works by iteratively solving

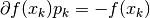
$\partial f(x_k)p_k = -f(x_k)$

and then updating as

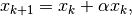
$x_{k+1} = x_k + \alpha x_k,$

where 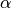$\alpha$ is a suitable step length (see the references). In this implementation the system of equations are solved using the conjugate gradient method.

References

[BV2004] Boyd, S, and Vandenberghe, L. Convex optimization. Cambridge university press, 2004.

[GNS2009] Griva, I, Nash, S G, and Sofer, A. Linear and nonlinear optimization. Siam, 2009.