broydens_method¶

odl.solvers.smooth.newton.broydens_method(f, x, line_search=1.0, impl='first', maxiter=1000, tol=1e-15, hessinv_estimate=None, callback=None)[source]¶

Broyden’s first method, a quasi-Newton scheme.

Parameters

fFunctional: Functional with f.gradient
xf.domain element: Starting point of the iteration
line_searchfloat or LineSearch, optional: Strategy to choose the step length. If a float is given, uses it as a fixed step length.
impl{‘first’, ‘second’}, optional: What version of Broydens method to use. First is also known as Broydens ‘good’ method, while the second is known as Broydens ‘bad’ method.
maxiterint, optional: Maximum number of iterations. tol.
tolfloat, optional: Tolerance that should be used for terminating the iteration.
hessinv_estimateOperator, optional: Initial estimate of the inverse of the Hessian operator. Needs to be an operator from f.domain to f.domain. Default: Identity on f.domain
callbackcallable, optional: Object executing code per iteration, e.g. plotting each iterate.

Notes

This is a general and optimized implementation of Broyden’s method, a quasi-Newton method for solving a general unconstrained optimization problem

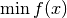
$\min f(x)$

for a differentiable function 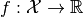$f: \mathcal{X}\to \mathbb{R}$ on a Hilbert space 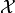$\mathcal{X}$ . It does so by finding a zero of the gradient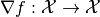

$\nabla f: \mathcal{X} \to \mathcal{X}$

using a Newton-type update scheme with approximate Hessian.

The algorithm is described in [Bro1965] and [Kva1991], and in a Wikipedia article.

References

[Bro1965] Broyden, C G. A class of methods for solving nonlinear simultaneous equations. Mathematics of computation, 33 (1965), pp 577–593.

[Kva1991] Kvaalen, E. A faster Broyden method. BIT Numerical Mathematics 31 (1991), pp 369–372.