steepest_descent¶

odl.solvers.smooth.gradient.steepest_descent(f, x, line_search=1.0, maxiter=1000, tol=1e-16, projection=None, callback=None)[source]¶

Steepest descent method to minimize an objective function.

General implementation of steepest decent (also known as gradient decent) for solving

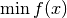
$\min f(x)$

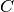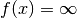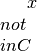The algorithm is intended for unconstrained problems. It needs line search in order guarantee convergence. With appropriate line search, it can also be used for constrained problems where one wants to minimize over some given set $C$ . This can be done by defining $f(x) = \infty$ for $x\\not\\in C$ , or by providing a projection function that projects the iterates on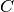 $C$ .

The algorithm is described in [BV2004], section 9.3--9.4 (book available online), [GNS2009], Section 12.2, and wikipedia Gradient_descent.

Parameters:

fFunctional: Goal functional. Needs to have f.gradient.
xf.domain element: Starting point of the iteration
line_searchfloat or LineSearch, optional: Strategy to choose the step length. If a float is given, uses it as a fixed step length.
maxiterint, optional: Maximum number of iterations.
tolfloat, optional: Tolerance that should be used for terminating the iteration.
projectioncallable, optional: Function that can be used to modify the iterates in each iteration, for example enforcing positivity. The function should take one argument and modify it in-place.
callbackcallable, optional: Object executing code per iteration, e.g. plotting each iterate