adam

odl.solvers.smooth.gradient.adam(f, x, learning_rate=0.001, beta1=0.9, beta2=0.999, eps=1e-08, maxiter=1000, tol=1e-16, callback=None)

ADAM method to minimize an objective function.

General implementation of ADAM for solving

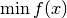
where 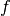is a differentiable functional.

The algorithm is described in [KB2015] (arxiv). All parameter names and default valuesare taken from the article.

Parameters:

fFunctional

Goal functional. Needs to have f.gradient.

xf.domain element

Starting point of the iteration, updated in place.

learning_ratepositive float, optional

Step length of the method.

beta1float in [0, 1), optional

Update rate for first order moment estimate.

beta2float in [0, 1), optional

Update rate for second order moment estimate.

epspositive float, optional

A small constant for numerical stability.

maxiterint, optional

Maximum number of iterations.

tolpositive float, optional

Tolerance that should be used for terminating the iteration.

callbackcallable, optional

Object executing code per iteration, e.g. plotting each iterate.

See also

odl.solvers.smooth.gradient.steepest_descent

Simple gradient descent.

odl.solvers.iterative.iterative.landweber

Optimized solver for the case f(x) = ||Ax - b||_2^2.

odl.solvers.iterative.iterative.conjugate_gradient

Optimized solver for the case f(x) = x^T Ax - 2 x^T b.

References

[KB2015] Kingma, D P and Ba, J. Adam: A Method for Stochastic Optimization, ICLR 2015.