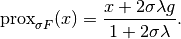proximal_l2_squared

odl.solvers.nonsmooth.proximal_operators.proximal_l2_squared(space, lam=1, g=None)[source]

Proximal operator factory of the squared l2-norm/distance.

Function for the proximal operator of the convex conjugate of the functional F where F is the l2-norm (or distance to g, if given):

F(x) =  lam ||x - g||_2^2

with x and g elements in space, scaling factor lam, and given data g.

Parameters
spaceLinearSpace

Domain of F(x). Needs to be a Hilbert space. That is, have an inner product (LinearSpace.inner).

lampositive float, optional

Scaling factor or regularization parameter.

gspace element, optional

An element in space. Default: space.zero.

Returns
prox_factoryfunction

Factory for the proximal operator to be initialized

See also

proximal_l2

proximal without square

proximal_convex_conj_l2_squared

proximal for convex conjugate

Notes

The squared 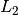L_2-norm/distance 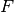F is given by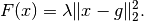

F(x) = \lambda \|x - g\|_2^2.

For a step size 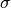\sigma, the proximal operator of 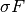\sigma F is given by

\mathrm{prox}_{\sigma F}(x) = \frac{x + 2 \sigma \lambda g} {1 + 2 \sigma \lambda}.