proximal_l2

odl.solvers.nonsmooth.proximal_operators.proximal_l2(space, lam=1, g=None)[source]

Proximal operator factory of the l2-norm/distance.

Function for the proximal operator of the functional F where F is the l2-norm (or distance to g, if given):

``F(x) =  lam ||x - g||_2``
Parameters:
spaceLinearSpace

Domain of F(x). Needs to be a Hilbert space. That is, have an inner product (LinearSpace.inner).

lampositive float, optional

Scaling factor or regularization parameter.

gspace element, optional

An element in space. Default: space.zero.

Returns:
prox_factorycallable

Factory for the proximal operator to be initialized.

See also

proximal_l2_squared

proximal for squared norm/distance

proximal_convex_conj_l2

proximal for convex conjugate

Notes

Most problems are forumlated for the squared norm/distance, in that case use proximal_l2_squared instead.

The 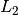L_2-norm/distance 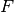F is given by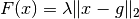

F(x) = \lambda \|x - g\|_2

For a step size 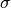\sigma, the proximal operator of 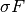\sigma F is given by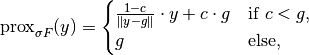

\mathrm{prox}_{\sigma F}(y) = \begin{cases} \frac{1 - c}{\|y-g\|} \cdot y + c \cdot g & \text{if } c < g, \\ g & \text{else}, \end{cases}

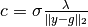where c = \sigma \frac{\lambda}{\|y - g\|_2}.