proximal_l1¶
- odl.solvers.nonsmooth.proximal_operators.proximal_l1(space, lam=1, g=None)[source]¶
Proximal operator factory of the L1 norm/distance.
Implements the proximal operator of the functional
F(x) = lam ||x - g||_1
with
xandgelements inspace, and scaling factorlam.- Parameters:
- space
LinearSpaceorProductSpace Domain of the functional.
- lampositive float, optional
Scaling factor or regularization parameter.
- g
spaceelement, optional Element to which the L1 distance is taken. Default:
space.zero.
- space
- Returns:
- prox_factoryfunction
Factory for the proximal operator to be initialized
See also
proximal_convex_conj_l1proximal for convex conjugate
proximal_l1_l2isotropic variant of the group L1 norm proximal
Notes
For the functional
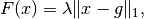
and a step size
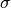 , the proximal operator of
, the proximal operator of
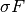 is given as the "soft-shrinkage" operator
is given as the "soft-shrinkage" operator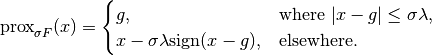
Here, all operations are to be read pointwise.
For vector-valued
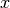 and
and 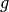 , the (non-isotropic) proximal
operator is the component-wise scalar proximal:
, the (non-isotropic) proximal
operator is the component-wise scalar proximal: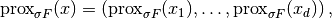
where
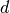 is the number of components of
is the number of components of 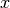 .
.