proximal_convex_conj_l1_l2

odl.solvers.nonsmooth.proximal_operators.proximal_convex_conj_l1_l2(space, lam=1, g=None)[source]

Proximal operator factory of the L1-L2 norm/distance convex conjugate.

Implements the proximal operator of the convex conjugate of the functional

F(x) = lam || |x - g|_2 ||_1

with x and g elements in space, and scaling factor lam. Here, |.|_2 is the pointwise Euclidean norm of a vector-valued function.

Parameters
spaceLinearSpace or ProductSpace of LinearSpace spaces

Domain of the functional F

lampositive float, optional

Scaling factor or regularization parameter.

gspace element, optional

Element to which the L1 distance is taken. Default: space.zero.

Returns
prox_factoryfunction

Factory for the proximal operator to be initialized.

See also

proximal_convex_conj_l1

Scalar or non-isotropic vectorial variant

Notes

The convex conjugate 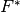F^* of the functional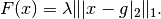

F(x) = \lambda \| |x - g|_2 \|_1.

is given by

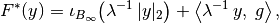
F^*(y) = \iota_{B_\infty} \big( \lambda^{-1}\, |y|_2 \big) + \left\langle \lambda^{-1}\, y,\: g \right\rangle,

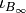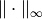where \iota_{B_\infty} is the indicator function of the unit ball with respect to \|\cdot\|_\infty.

For a step size 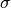\sigma, the proximal operator of 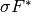\sigma F^* is given by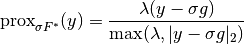

\mathrm{prox}_{\sigma F^*}(y) = \frac{\lambda (y - \sigma g)}{ \max(\lambda, |y - \sigma g|_2)}

Here, all operations are to be read pointwise.