prox_dca¶

odl.solvers.nonsmooth.difference_convex.prox_dca(x, f, g, niter, gamma, callback=None)[source]¶

Proximal DCA of Sun, Sampaio and Candido.

This algorithm solves a problem of the form

min_x f(x) - g(x)

where f and g are two proper, convex and lower semicontinuous functions.

Parameters:

xLinearSpaceElement: Initial point, updated in-place.
fFunctional: Convex functional. Needs to implement f.proximal.
gFunctional: Convex functional. Needs to implement g.gradient.
niterint: Number of iterations.
gammapositive float: Stepsize in the primal updates.
callbackcallable, optional: Function called with the current iterate after each iteration.

See also

dca: Solver with subgradinet steps for all the functionals.
doubleprox_dc: Solver with proximal steps for all the nonsmooth convex functionals and a gradient step for a smooth functional.

Notes

The algorithm was proposed as Algorithm 2.3 in [SSC2003]. It solves the problem

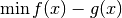
$\min f(x) - g(x)$

by using subgradients of 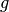$g$ and proximal points of 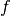$f$ . The iteration is given by

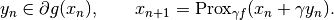
$y_n \in \partial g(x_n), \qquad x_{n+1} = \mathrm{Prox}_{\gamma f}(x_n + \gamma y_n).$

In contrast to dca, prox_dca uses proximal steps with respect to the convex part f. Both algorithms use subgradients of the concave part g.

References

[SSC2003] Sun, W, Sampaio R J B, and Candido M A B. Proximal point algorithm for minimization of DC function. Journal of Computational Mathematics, 21.4 (2003), pp 451--462.