doubleprox_dc

odl.solvers.nonsmooth.difference_convex.doubleprox_dc(x, y, f, phi, g, K, niter, gamma, mu, callback=None)[source]

Double-proxmial gradient d.c. algorithm of Banert and Bot.

This algorithm solves a problem of the form

min_x f(x) + phi(x) - g(Kx).
Parameters
xLinearSpaceElement

Initial primal guess, updated in-place.

yLinearSpaceElement

Initial dual guess, updated in-place.

fFunctional

Convex functional. Needs to implement g.proximal.

phiFunctional

Convex functional. Needs to implement phi.gradient. Convergence can be guaranteed if the gradient is Lipschitz continuous.

gFunctional

Convex functional. Needs to implement h.convex_conj.proximal.

KOperator

Linear operator. Needs to implement K.adjoint

niterint

Number of iterations.

gammapositive float

Stepsize in the primal updates.

mupositive float

Stepsize in the dual updates.

callbackcallable, optional

Function called with the current iterate after each iteration.

See also

dca

Solver with subgradient steps for all the functionals.

prox_dca

Solver with a proximal step for f and a subgradient step for g.

Notes

This algorithm is proposed in [BB2016] and solves the d.c. problem

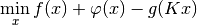
\min_x f(x) + \varphi(x) - g(Kx)

together with its Toland dual

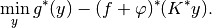
\min_y g^*(y) - (f + \varphi)^*(K^* y).

The iterations are given by

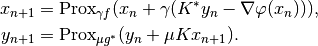
x_{n+1} &= \mathrm{Prox}_{\gamma f} (x_n + \gamma (K^* y_n - \nabla \varphi(x_n))), \\ y_{n+1} &= \mathrm{Prox}_{\mu g^*} (y_n + \mu K x_{n+1}).

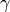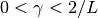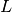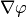To guarantee convergence, the parameter \gamma must satisfy 0 < \gamma < 2/L where L is the Lipschitz constant of \nabla \varphi.

References

[BB2016] Banert, S, and Bot, R I. A general double-proximal gradient algorithm for d.c. programming. arXiv:1610.06538 [math.OC] (2016).