RosenbrockFunctional¶

class odl.solvers.functional.example_funcs.RosenbrockFunctional(*args, **kwargs)[source]¶

Bases: Functional

The well-known Rosenbrock function on R^n.

The Rosenbrock function is often used as a test problem in smooth optimization.

Notes

The functional is defined for 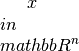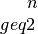$x \\in \\mathbb{R}^n$ , $n \\geq 2$ , as

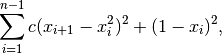
$\sum_{i=1}^{n - 1} c (x_{i+1} - x_i^2)^2 + (1 - x_i)^2,$

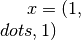where $c$ is a constant, usually set to 100, which determines how "ill-behaved" the function should be. The global minimum lies at $x = (1, \\dots, 1)$ , independent of $c$ .

There are two definitions of the n-dimensional Rosenbrock function found in the literature. One is the product of 2-dimensional Rosenbrock functions, which is not the one used here. This one extends the pattern of the 2d Rosenbrock function so all dimensions depend on each other in sequence.

References

Attributes:

adjoint: Adjoint of this operator (abstract).
convex_conj: Convex conjugate functional of the functional.
domain: Set of objects on which this operator can be evaluated.
grad_lipschitz: Lipschitz constant for the gradient of the functional.
gradient: Gradient operator of the Rosenbrock functional.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
proximal: Proximal factory of the functional.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`bregman`(point, subgrad)	Return the Bregman distance functional.
`derivative`(point)	Return the derivative operator in the given point.
`norm`([estimate])	Return the operator norm of this operator.
`translated`(shift)	Return a translation of the functional.

__init__(space, scale=100.0)[source]¶

Initialize a new instance.

Parameters:

spaceTensorSpace: Domain of the functional.
scalepositive float, optional: The scale c in the functional determining how "ill-behaved" the functional should be. Larger value means worse behavior.

Examples

Initialize and call the functional:

>>> r2 = odl.rn(2)
>>> functional = RosenbrockFunctional(r2)
>>> functional([1, 1])  # optimum is 0 at [1, 1]
0.0
>>> functional([0, 1])
101.0

The functional can also be used in higher dimensions:

>>> r5 = odl.rn(5)
>>> functional = RosenbrockFunctional(r5)
>>> functional([1, 1, 1, 1, 1])
0.0

We can change how much the function is ill-behaved via scale:

>>> r2 = odl.rn(2)
>>> functional = RosenbrockFunctional(r2, scale=2)
>>> functional([1, 1])  # optimum is still 0 at [1, 1]
0.0
>>> functional([0, 1])  # much lower variation
3.0