IdentityFunctional.proximal¶

property IdentityFunctional.proximal¶

Proximal factory of the functional.

Notes

The proximal operator of a function 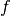$f$ is an operator defined as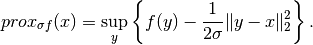

$prox_{\sigma f}(x) = \sup_{y} \left\{ f(y) - \frac{1}{2\sigma} \| y-x \|_2^2 \right\}.$

Proximal operators are often used in different optimization algorithms, especially when designed to handle nonsmooth functionals.

A proximal factory is a function that, when called with a step length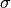 $\sigma$ , returns the corresponding proximal operator.

The nonsmooth solvers that make use of proximal operators to solve a given optimization problem take a proximal factory as input, i.e., a function returning a proximal operator. See for example forward_backward_pd.

In general, the step length 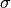$\sigma$ is expected to be a positive float, but certain functionals might accept more types of objects as a stepsize:

If a functional is a SeparableSum, then, instead of a positive float, one may call the proximal factory with a list of positive floats, and the stepsize are applied to each component individually.
For certain special functionals like L1Norm and L2NormSquared, which are not implemented as a SeparableSum, the proximal factory will accept an argument which is element-like regarding the domain of the functional. Its components must be strictly positive floats.

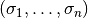A stepsize like $(\sigma_1, \ldots, \sigma_n)$ coincides with a matrix-valued distance according to Section XV.4 of [HL1993] and the rule

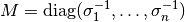
$M = \mathrm{diag}(\sigma_1^{-1}, \ldots, \sigma_n^{-1})$

or the Bregman-proximal according to [E1993] and the rule

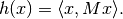
$h(x) = \langle x, M x \rangle.$

References

[HL1993] Hiriart-Urruty J-B, and Lemaréchal C. Convex analysis and minimization algorithms II. Advanced theory and bundle methods. Springer, 1993.

[E1993] Eckstein J. Nonlinear proximal point algorithms using Bregman functions, with applications to convex programming. Mathematics of Operations Research, 18.1 (1993), pp 202--226.