MatrixOperator¶

class odl.operator.tensor_ops.MatrixOperator(*args, **kwargs)[source]¶

Bases: Operator

A matrix acting as a linear operator.

This operator uses a matrix to represent an operator, and get its adjoint and inverse by doing computations on the matrix. This is in general a rather slow and memory-inefficient approach, and users are recommended to use other alternatives if possible.

Attributes:

adjoint: Adjoint operator represented by the adjoint matrix.
axis: Axis of domain elements over which is summed.
domain: Set of objects on which this operator can be evaluated.
inverse: Inverse operator represented by the inverse matrix.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
matrix: Matrix representing this operator.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`derivative`(point)	Return the operator derivative at `point`.
`norm`([estimate])	Return the operator norm of this operator.

__init__(matrix, domain=None, range=None, axis=0)[source]¶

Initialize a new instance.

Parameters:

matrixarray-like or scipy.sparse.base.spmatrix: 2-dimensional array representing the linear operator. For Scipy sparse matrices only tensor spaces with ndim == 1 are allowed as domain.
domainTensorSpace, optional: Space of elements on which the operator can act. Its dtype must be castable to range.dtype. For the default None, a space with 1 axis and size matrix.shape[1] is used, together with the matrix' data type.
rangeTensorSpace, optional: Space of elements on to which the operator maps. Its shape and dtype attributes must match those of the result of the multiplication. For the default None, the range is inferred from matrix, domain and axis.
axisint, optional: Sum over this axis of an input tensor in the multiplication.

Notes

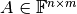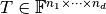For a matrix $A \in \mathbb{F}^{n \times m}$ , the operation on a tensor $T \in \mathbb{F}^{n_1 \times \dots \times n_d}$ is defined as the summation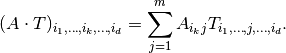

$(A \cdot T)_{i_1, \dots, i_k, \dots, i_d} = \sum_{j=1}^m A_{i_k j} T_{i_1, \dots, j, \dots, i_d}.$

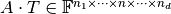It produces a new tensor $A \cdot T \in \mathbb{F}^{ n_1 \times \dots \times n \times \dots \times n_d}$ .

Examples

By default, domain and range are spaces of with one axis:

>>> m = np.ones((3, 4))
>>> op = MatrixOperator(m)
>>> op.domain
rn(4)
>>> op.range
rn(3)
>>> op([1, 2, 3, 4])
rn(3).element([ 10.,  10.,  10.])

For multi-dimensional arrays (tensors), the summation (contraction) can be performed along a specific axis. In this example, the number of matrix rows (4) must match the domain shape entry in the given axis:

>>> dom = odl.rn((5, 4, 4))  # can use axis=1 or axis=2
>>> op = MatrixOperator(m, domain=dom, axis=1)
>>> op(dom.one()).shape
(5, 3, 4)
>>> op = MatrixOperator(m, domain=dom, axis=2)
>>> op(dom.one()).shape
(5, 4, 3)

The operator also works on uniform_discr type spaces. Note, however, that the weighting of the domain is propagated to the range by default, in order to keep the correspondence between adjoint and transposed matrix:

>>> space = odl.uniform_discr(0, 1, 4)
>>> op = MatrixOperator(m, domain=space)
>>> op(space.one())
rn(3, weighting=0.25).element([ 4.,  4.,  4.])
>>> np.array_equal(op.adjoint.matrix, m.T)
True