WeightedSumSamplingOperator

class odl.operator.tensor_ops.WeightedSumSamplingOperator(*args, **kwargs)

Bases: odl.operator.operator.Operator

Operator computing the sum of coefficients at sampling locations.

This operator is the adjoint of SamplingOperator.

Notes

The weighted sum sampling operator for a sequence 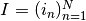of indices (possibly with duplicates) is given by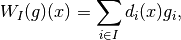

where 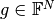is the value vector, and 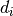is either a Dirac delta or a characteristic function of the cell centered around the point indexed by .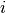

Attributes

adjoint

Adjoint of this operator, a SamplingOperator.

domain

Set of objects on which this operator can be evaluated.

inverse

Return the operator inverse.

is_functional

True if this operator’s range is a Field.

is_linear

True if this operator is linear.

range

Set in which the result of an evaluation of this operator lies.

sampling_points

Indices where to sample the function.

variant

Weighting scheme for the operator.

Methods

_call(self, x)	Sum all values if indices are given multiple times.
derivative(self, point)	Return the operator derivative at point.
norm(self[, estimate])	Return the operator norm of this operator.

__init__(self, range, sampling_points, variant='char_fun')

Initialize a new instance.

Parameters

rangeTensorSpace

Set of elements into which this operator maps.

sampling_points1D array-like or sequence of 1D array-likes

Indices that determine the sampling points. In n dimensions, it should be a sequence of n arrays, where each member array is of equal length N. The indexed positions are (arr1[i], arr2[i], ..., arrn[i]), in total N points. If range is one-dimensional, a single array-like can be used. Likewise, a single point can be given as integer in 1D, and as a array-like sequence in nD.

variant{‘char_fun’, ‘dirac’}, optional

This option determines which function to sum over.

Examples

In 1d, a single index (an int) or a sequence of such can be used for indexing.

>>> space = odl.uniform_discr(0, 1, 4)
>>> op = odl.WeightedSumSamplingOperator(space, sampling_points=1)
>>> op.domain
rn(1)
>>> x = op.domain.element([1])
>>> # Put value 1 at index 1
>>> op(x)
uniform_discr(0.0, 1.0, 4).element([ 0.,  1.,  0.,  0.])
>>> op = odl.WeightedSumSamplingOperator(space,
...                                      sampling_points=[1, 2, 1])
>>> op.domain
rn(3)
>>> x = op.domain.element([1, 0.5, 0.25])
>>> # Index 1 occurs twice and gets two contributions (1 and 0.25)
>>> op(x)
uniform_discr(0.0, 1.0, 4).element([ 0.  ,  1.25,  0.5 ,  0.  ])

The 'dirac' variant scales the values by the reciprocal cell volume of the operator range:

>>> op = odl.WeightedSumSamplingOperator(
...     space, sampling_points=[1, 2, 1], variant='dirac')
>>> x = op.domain.element([1, 0.5, 0.25])
>>> 1 / op.range.cell_volume  # the scaling constant
4.0
>>> op(x)
uniform_discr(0.0, 1.0, 4).element([ 0.,  5.,  2.,  0.])

In higher dimensions, a sequence of index array-likes must be given, or a single sequence for a single point:

>>> space = odl.uniform_discr([0, 0], [1, 1], (2, 3))
>>> # Sample at the index (0, 2)
>>> op = odl.WeightedSumSamplingOperator(space,
...                                      sampling_points=[0, 2])
>>> x = op.domain.element([1])
>>> # Insert the value 1 at index (0, 2)
>>> op(x)
uniform_discr([ 0.,  0.], [ 1.,  1.], (2, 3)).element(
    [[ 0.,  0.,  1.],
     [ 0.,  0.,  0.]]
)
>>> sampling_points = [[0, 1],  # indices (0, 2) and (1, 1)
...                    [2, 1]]
>>> op = odl.WeightedSumSamplingOperator(space, sampling_points)
>>> x = op.domain.element([1, 2])
>>> op(x)
uniform_discr([ 0.,  0.], [ 1.,  1.], (2, 3)).element(
    [[ 0.,  0.,  1.],
     [ 0.,  2.,  0.]]
)