Primal-Dual Hybrid Gradient Algorithm (PDHG)¶
This page introduces the mathematics behind the Primal-Dual Hybrid Gradient Algorithm. For an applied point of view, please see the user's guide to this method.
The general problem¶
The Primal-Dual Hybrid Gradient Algorithm (PDHG) algorithm, as studied in [CP2011a], is a first order method for non-smooth convex optimization problems with known saddle-point structure
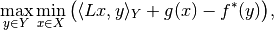
where 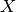 and
and 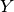 are Hilbert spaces with inner product
are Hilbert spaces with inner product 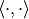 and norm
and norm 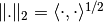 ,
, 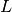 is a continuous linear operator
is a continuous linear operator 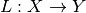 ,
, ![g: X \to [0,+\infty]](../../../_images/math/0c5f4e78f54d4ab9d228b8b2784f9343359d6316.png) and
and ![f: Y \to [0,+\infty]](../../../_images/math/caca634b0873b1c7090317209b869db9001d44be.png) are proper, convex and lower semi-continuous functionals, and
are proper, convex and lower semi-continuous functionals, and 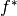 is the convex (or Fenchel) conjugate of f, (see convex conjugate).
is the convex (or Fenchel) conjugate of f, (see convex conjugate).
The saddle-point problem is a primal-dual formulation of the primal minimization problem
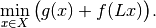
The corresponding dual maximization problem is
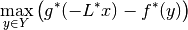
with 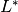 being the adjoint of the operator
being the adjoint of the operator 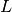 .
.
The algorithm¶
PDHG basically consists in alternating a gradient-like ascent in the dual variable 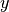 and a gradient-like descent in the primal variable
and a gradient-like descent in the primal variable 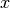 .
Additionally, an over-relaxation in the primal variable is performed.
.
Additionally, an over-relaxation in the primal variable is performed.
Initialization¶
Choose 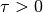 ,
,  ,
, ![\theta \in [0,1]](../../../_images/math/945ffffedefdf26c41830e437501956e8202eebf.png) ,
,
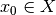 ,
, 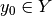 ,
, 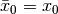
Iteration¶
For  update
update 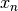 ,
, 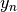 , and
, and 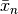 as
follows:
as
follows:
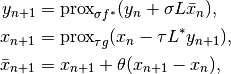
Here, 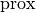 stands for proximal operator.
stands for proximal operator.
Step sizes¶
A simple choice of step size parameters is 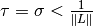 , since the requirement
, since the requirement 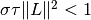 guarantees convergence of the algorithm.
Of course, this does not imply that this choice is anywhere near optimal, but it can serve as a good starting point.
guarantees convergence of the algorithm.
Of course, this does not imply that this choice is anywhere near optimal, but it can serve as a good starting point.
Acceleration¶
If 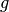 or
or 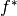 is uniformly convex, convergence can be accelerated using variable step sizes as follows:
is uniformly convex, convergence can be accelerated using variable step sizes as follows:
Replace 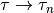 ,
, 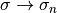 , and
, and 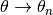 and choose
and choose 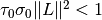 and
and 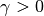 .
After the update of the primal variable
.
After the update of the primal variable 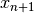 and before the update of the relaxation variable
and before the update of the relaxation variable 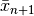 use the following update scheme for relaxation and step size parameters:
use the following update scheme for relaxation and step size parameters:
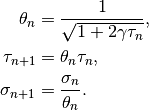
Instead of choosing step size parameters, preconditioning techniques can be employed, see [CP2011b].
In this case the steps 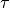 and
and 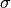 are replaced by symmetric and positive definite matrices
are replaced by symmetric and positive definite matrices 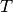 and
and 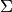 , respectively, and convergence holds for
, respectively, and convergence holds for 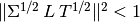 .
.
For more on proximal operators and algorithms see [PB2014]. The implementation of PDHG in ODL is along the lines of [Sid+2012].