conjugate_gradient_nonlinear

odl.solvers.smooth.nonlinear_cg.conjugate_gradient_nonlinear(f, x, line_search=1.0, maxiter=1000, nreset=0, tol=1e-16, beta_method='FR', callback=None)

Conjugate gradient for nonlinear problems.

Parameters:

fFunctional

Functional with f.gradient.

xop.domain element

Vector to which the result is written. Its initial value is used as starting point of the iteration, and its values are updated in each iteration step.

line_searchfloat or LineSearch, optional

Strategy to choose the step length. If a float is given, it is used as a fixed step length.

maxiterint, optional

Maximum number of iterations to perform.

nresetint, optional

Number of times the solver should be reset. Default: no reset.

tolfloat, optional

Tolerance that should be used to terminating the iteration.

beta_method{'FR', 'PR', 'HS', 'DY'}, optional

Method to calculate beta in the iterates.

• 'FR' : Fletcher-Reeves

• 'PR' : Polak-Ribiere

• 'HS' : Hestenes-Stiefel

• 'DY' : Dai-Yuan

callbackcallable, optional

Object executing code per iteration, e.g. plotting each iterate.

See also

odl.solvers.smooth.newton.bfgs_method

Quasi-Newton solver for the same problem

odl.solvers.iterative.iterative.conjugate_gradient

Optimized solver for least-squares problem with linear and symmetric operator

odl.solvers.iterative.iterative.conjugate_gradient_normal

Equivalent solver but for least-squares problem with linear operator

Notes

This is a general and optimized implementation of the nonlinear conjguate gradient method for solving a general unconstrained optimization problem

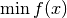
for a differentiable functional 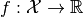on a Hilbert space 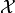. It does so by finding a zero of the gradient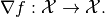

The method is described in a Wikipedia article.