proximal_quadratic_perturbation¶

odl.solvers.nonsmooth.proximal_operators.proximal_quadratic_perturbation(prox_factory, a, u=None)[source]¶

Calculate the proximal of function F(x) + a * |x|^2 + <u,x>.

Parameters

prox_factorycallable: A factory function that, when called with a step size, returns the proximal operator of F
anon-negative float: Scaling of the quadratic term
uElement in domain of F, optional: Defines the linear functional. For None, the zero element is taken.

Returns

prox_factoryfunction: Factory for the proximal operator to be initialized

Notes

Given a functional 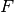$F$ , this is calculated according to the rule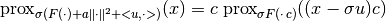

$\mathrm{prox}_{\sigma \left(F( \cdot ) + a \| \cdot \|^2 + <u, \cdot >\right)}(x) = c \; \mathrm{prox}_{\sigma F( \cdot \, c)}((x - \sigma u) c)$

where $c$ is the constant

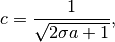
$c = \frac{1}{\sqrt{2 \sigma a + 1}},$

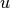$a$ is the scaling parameter belonging to the quadratic term, $u$ is the space element defining the linear functional, and 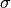$\sigma$ is the step size.

For reference on the identity used, see [CP2011c]. Note that this identity is not the exact one given in the reference, but was recalculated for arbitrary step lengths.

References

[CP2011c] Combettes, P L, and Pesquet, J-C. Proximal splitting methods in signal processing. In: Bauschke, H H, Burachik, R S, Combettes, P L, Elser, V, Luke, D R, and Wolkowicz, H. Fixed-point algorithms for inverse problems in science and engineering, Springer, 2011.