proximal_convex_conj¶

odl.solvers.nonsmooth.proximal_operators.proximal_convex_conj(prox_factory)[source]¶

Calculate the proximal of the dual using Moreau decomposition.

Parameters:

prox_factorycallable: A factory function that, when called with a step size, returns the proximal operator of F

Returns:

prox_factoryfunction: Factory for the proximal operator to be initialized

Notes

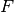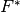The Moreau identity states that for any convex function $F$ with convex conjugate $F^*$ , the proximals satisfy

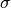$\mathrm{prox}_{\sigma F^*}(x) +\sigma \, \mathrm{prox}_{F / \sigma}(x / \sigma) = x$

where $\sigma$ is a scalar step size. Using this, the proximal of the convex conjugate is given by

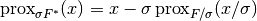
$\mathrm{prox}_{\sigma F^*}(x) = x - \sigma \, \mathrm{prox}_{F / \sigma}(x / \sigma)$

Note that since 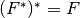$(F^*)^* = F$ , this can be used to get the proximal of the original function from the proximal of the convex conjugate.

For reference on the Moreau identity, see [CP2011c].

References

[CP2011c] Combettes, P L, and Pesquet, J-C. Proximal splitting methods in signal processing. In: Bauschke, H H, Burachik, R S, Combettes, P L, Elser, V, Luke, D R, and Wolkowicz, H. Fixed-point algorithms for inverse problems in science and engineering, Springer, 2011.