mlem

odl.solvers.iterative.statistical.mlem(op, x, data, niter, callback=None, **kwargs)

Maximum Likelihood Expectation Maximation algorithm.

Attempts to solve:

max_x L(x | data)

where L(x | data) is the Poisson likelihood of x given data. The likelihood depends on the forward operator op such that (approximately):

op(x) = data

Parameters:

opOperator

Forward operator in the inverse problem.

xop.domain element

Vector to which the result is written. Its initial value is used as starting point of the iteration, and its values are updated in each iteration step. The initial value of x should be non-negative.

dataop.range element-like

Right-hand side of the equation defining the inverse problem.

niterint

Number of iterations.

callbackcallable, optional

Function called with the current iterate after each iteration.

Other Parameters:

sensitivitiesfloat or op.domain element-like, optional

The algorithm contains a A^T 1 term, if this parameter is given, it is replaced by it. Default: op.adjoint(op.range.one())

See also

osmlem

Ordered subsets MLEM

loglikelihood

Function for calculating the logarithm of the likelihood

Notes

Given a forward model 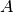and data 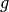, the algorithm attempts to find an 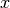that maximizes: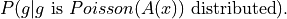

The algorithm is explicitly given by: