landweber¶
- odl.solvers.iterative.iterative.landweber(op, x, rhs, niter, omega=None, projection=None, callback=None)[source]¶
Optimized implementation of Landweber's method.
Solves the inverse problem:
A(x) = rhs
- Parameters:
- op
Operator Operator in the inverse problem.
op.derivative(x).adjointmust be well-defined forxin the operator domain.- x
op.domainelement Element to which the result is written. Its initial value is used as starting point of the iteration, and its values are updated in each iteration step.
- rhs
op.rangeelement Right-hand side of the equation defining the inverse problem.
- niterint
Number of iterations.
- omegapositive float, optional
Relaxation parameter in the iteration. Default:
1 / op.norm(estimate=True) ** 2- projectioncallable, optional
Function that can be used to modify the iterates in each iteration, for example enforcing positivity. The function should take one argument and modify it in-place.
- callbackcallable, optional
Object executing code per iteration, e.g. plotting each iterate.
- op
Notes
This method calculates an approximate least-squares solution of the inverse problem of the first kind

for a given
 , i.e. an approximate
solution
, i.e. an approximate
solution 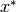 to
to
for a (Frechet-) differentiable operator
 between Hilbert
spaces
between Hilbert
spaces 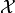 and
and  . The method
starts from an initial guess
. The method
starts from an initial guess 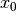 and uses the
iteration
and uses the
iteration
where
 is the Frechet derivative
of
is the Frechet derivative
of  at
at 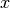 and
and  is a
relaxation parameter. For linear problems, a choice
is a
relaxation parameter. For linear problems, a choice
 guarantees
convergence, where
guarantees
convergence, where  stands for the
operator norm of
stands for the
operator norm of  .
.Users may also optionally provide a projection to project each iterate onto some subset. For example enforcing positivity.
This implementation uses a minimum amount of memory copies by applying re-usable temporaries and in-place evaluation.
The method is also described in a Wikipedia article.