kaczmarz¶
- odl.solvers.iterative.iterative.kaczmarz(ops, x, rhs, niter, omega=1, projection=None, random=False, callback=None, callback_loop='outer')[source]¶
Optimized implementation of Kaczmarz's method.
Solves the inverse problem given by the set of equations:
A_n(x) = rhs_n
This is also known as the Landweber-Kaczmarz's method, since the method coincides with the Landweber method for a single operator.
- Parameters:
- opssequence of
Operator's Operators in the inverse problem.
op[i].derivative(x).adjointmust be well-defined forxin the operator domain and for alli.- x
op.domainelement Element to which the result is written. Its initial value is used as starting point of the iteration, and its values are updated in each iteration step.
- rhssequence of
ops[i].rangeelements Right-hand side of the equation defining the inverse problem.
- niterint
Number of iterations.
- omegapositive float or sequence of positive floats, optional
Relaxation parameter in the iteration. If a single float is given the same step is used for all operators, otherwise separate steps are used.
- projectioncallable, optional
Function that can be used to modify the iterates in each iteration, for example enforcing positivity. The function should take one argument and modify it in-place.
- randombool, optional
If
True, the order of the operators is randomized in each iteration.- callbackcallable, optional
Object executing code per iteration, e.g. plotting each iterate.
- callback_loop{'inner', 'outer'}
Whether the callback should be called in the inner or outer loop.
- opssequence of
See also
Notes
This method calculates an approximate least-squares solution of the inverse problem of the first kind
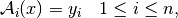
for a given
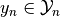 , i.e. an approximate
solution
, i.e. an approximate
solution 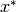 to
to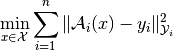
for a (Frechet-) differentiable operator
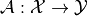 between Hilbert
spaces
between Hilbert
spaces 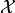 and
and 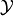 . The method
starts from an initial guess
. The method
starts from an initial guess 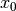 and uses the
iteration
and uses the
iteration![x_{k+1} = x_k - \omega_{[k]} \ \partial \mathcal{A}_{[k]}(x_k)^*
(\mathcal{A}_{[k]}(x_k) - y_{[k]}),](../_images/math/fb2ea8fda8f4820d5f0c12982a5ab333bc9e5941.png)
where
![\partial \mathcal{A}_{[k]}(x_k)](../_images/math/861d3fdf8523fbf123010540f2a06d62fc2d8f98.png) is the Frechet derivative
of
is the Frechet derivative
of ![\mathcal{A}_{[k]}](../_images/math/b58a36f1b6da4420380ce1d3117a6bee89b15a45.png) at
at 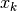 ,
, ![\omega_{[k]}](../_images/math/b39c41908336a641febb52ecc602457f4b6a4524.png) is a
relaxation parameter and
is a
relaxation parameter and ![[k] := k \text{ mod } n](../_images/math/5392f0aeb4b79850d543d7278095764abaf4a45f.png) .
.For linear problems, a choice
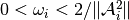 guarantees
convergence, where
guarantees
convergence, where 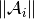 stands for the
operator norm of
stands for the
operator norm of 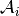 .
.This implementation uses a minimum amount of memory copies by applying re-usable temporaries and in-place evaluation.
The method is also described in a Wikipedia article. and in Natterer, F. Mathematical Methods in Image Reconstruction, section 5.3.2.