NumericalGradient¶

class odl.solvers.functional.derivatives.NumericalGradient(*args, **kwargs)[source]¶

Bases: Operator

The gradient of a Functional computed by finite differences.

See also

NumericalDerivative: Compute directional derivative

Attributes:

adjoint: Adjoint of this operator (abstract).
domain: Set of objects on which this operator can be evaluated.
inverse: Return the operator inverse.
is_functional: True if this operator's range is a Field.
is_linear: True if this operator is linear.
range: Set in which the result of an evaluation of this operator lies.

Methods

`__call__`(x[, out])	Return `self(x[, out, **kwargs])`.
`derivative`(point)	Return the derivative in `point`.
`norm`([estimate])	Return the operator norm of this operator.

__init__(functional, method='forward', step=None)[source]¶

Initialize a new instance.

Parameters:

functionalFunctional: The functional whose gradient should be computed. Its domain must be a TensorSpace.
method{'backward', 'forward', 'central'}, optional: The method to use to compute the gradient.
stepfloat, optional: The step length used in the derivative computation. Default: selects the step according to the dtype of the space.

Notes

If the functional is 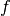$f$ and step size 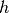$h$ is used, the gradient is computed as follows.

method='backward':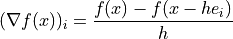

$(\nabla f(x))_i = \frac{f(x) - f(x - h e_i)}{h}$

method='forward':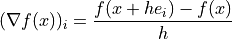

$(\nabla f(x))_i = \frac{f(x + h e_i) - f(x)}{h}$

method='central':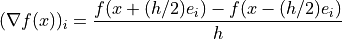

$(\nabla f(x))_i = \frac{f(x + (h/2) e_i) - f(x - (h/2) e_i)}{h}$

The number of function evaluations is functional.domain.size + 1 if 'backward' or 'forward' is used and 2 * functional.domain.size if 'central' is used. On large domains this will be computationally infeasible.

Examples

>>> space = odl.rn(3)
>>> func = odl.solvers.L2NormSquared(space)
>>> grad = NumericalGradient(func)
>>> grad([1, 1, 1])
rn(3).element([ 2.,  2.,  2.])

The gradient gives the correct value with sufficiently small step size:

>>> grad([1, 1, 1]) == func.gradient([1, 1, 1])
True

If the step is too large the result is not correct:

>>> grad = NumericalGradient(func, step=0.5)
>>> grad([1, 1, 1])
rn(3).element([ 2.5,  2.5,  2.5])

But it can be improved by using the more accurate method='central':

>>> grad = NumericalGradient(func, method='central', step=0.5)
>>> grad([1, 1, 1])
rn(3).element([ 2.,  2.,  2.])