NumericalDerivative¶
- class odl.solvers.functional.derivatives.NumericalDerivative(*args, **kwargs)[source]¶
Bases:
OperatorThe derivative of an operator by finite differences.
See also
NumericalGradientCompute gradient of a functional
- Attributes:
adjointAdjoint of this operator (abstract).
domainSet of objects on which this operator can be evaluated.
inverseReturn the operator inverse.
is_functionalTrueif this operator's range is aField.is_linearTrueif this operator is linear.rangeSet in which the result of an evaluation of this operator lies.
Methods
__call__(x[, out])Return
self(x[, out, **kwargs]).derivative(point)Return the operator derivative at
point.norm([estimate])Return the operator norm of this operator.
- __init__(operator, point, method='forward', step=None)[source]¶
Initialize a new instance.
- Parameters:
- operator
Operator The operator whose derivative should be computed numerically. Its domain and range must be
TensorSpacespaces.- point
operator.domainelement-like The point to compute the derivative in.
- method{'backward', 'forward', 'central'}, optional
The method to use to compute the derivative.
- stepfloat, optional
The step length used in the derivative computation. Default: selects the step according to the dtype of the space.
- operator
Notes
If the operator is
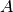 and step size
and step size 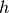 is used, the
derivative in the point
is used, the
derivative in the point 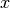 and direction
and direction 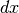 is computed
as follows.
is computed
as follows.method='backward':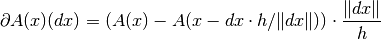
method='forward':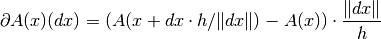
method='central':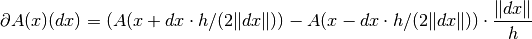
The number of operator evaluations is
2, regardless of parameters.Examples
Compute a numerical estimate of the derivative (Hessian) of the squared L2 norm:
>>> space = odl.rn(3) >>> func = odl.solvers.L2NormSquared(space) >>> hess = NumericalDerivative(func.gradient, [1, 1, 1]) >>> hess([0, 0, 1]) rn(3).element([ 0., 0., 2.])
Find the Hessian matrix:
>>> hess_matrix = odl.matrix_representation(hess) >>> np.allclose(hess_matrix, 2 * np.eye(3)) True