NumpyTensorSpaceConstWeighting¶

class odl.space.npy_tensors.NumpyTensorSpaceConstWeighting(const, exponent=2.0)[source]¶

Weighting of a NumpyTensorSpace by a constant.

See Notes for mathematical details.

Attributes:

Methods

`dist`(x1, x2)	Return the weighted distance between `x1` and `x2`.
`equiv`(other)	Test if other is an equivalent weighting.
`inner`(x1, x2)	Return the weighted inner product of `x1` and `x2`.
`norm`(x)	Return the weighted norm of `x`.

__init__(const, exponent=2.0)[source]¶

Initialize a new instance.

Parameters:

constpositive float: Weighting constant of the inner product, norm and distance.
exponentpositive float: Exponent of the norm. For values other than 2.0, the inner product is not defined.

Notes

For exponent 2.0, a new weighted inner product with constant $c$ is defined as

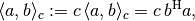
$\langle a, b\rangle_c := c \, \langle a, b\rangle_c = c \, b^{\mathrm{H}} a,$

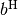where $b^{\mathrm{H}}$ standing for transposed complex conjugate.
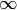For other exponents, only norm and dist are defined. In the case of exponent $\infty$ , the weighted norm is defined as

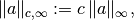
$\| a \|_{c, \infty} := c\, \| a \|_{\infty},$

otherwise it is

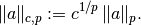
$\| a \|_{c, p} := c^{1/p}\, \| a \|_{p}.$
Note that this definition does not fulfill the limit property in 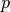$p$ , i.e.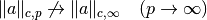

$\| a\|_{c, p} \not\to \| a \|_{c, \infty} \quad (p \to \infty)$

unless $c = 1$ .
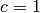The constant must be positive, otherwise it does not define an inner product or norm, respectively.