FunctionalQuadraticPerturb.convex_conj¶
- property FunctionalQuadraticPerturb.convex_conj¶
Convex conjugate functional of the functional.
Notes
Given a functional
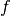 , the convex conjugate of a linearly
perturbed version
, the convex conjugate of a linearly
perturbed version 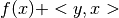 is given by a translation of
the convex conjugate of
is given by a translation of
the convex conjugate of 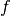 :
: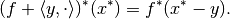
For reference on the identity used, see [KP2015]. Moreover, the convex conjugate of
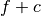 is by definition
is by definition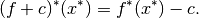
References
[KP2015] Komodakis, N, and Pesquet, J-C. Playing with Duality: An overview of recent primal-dual approaches for solving large-scale optimization problems. IEEE Signal Processing Magazine, 32.6 (2015), pp 31--54.