power_method_opnorm¶

odl.operator.oputils.power_method_opnorm(op, xstart=None, maxiter=100, rtol=1e-05, atol=1e-08, callback=None)[source]¶

Estimate the operator norm with the power method.

Parameters

opOperator: Operator whose norm is to be estimated. If its Operator.range range does not coincide with its Operator.domain, an Operator.adjoint must be defined (which implies that the operator must be linear).
xstartop.domain element-like, optional: Starting point of the iteration. By default an Operator.domain element containing noise is used.
maxiterpositive int, optional: Number of iterations to perform. If the domain and range of op do not match, it needs to be an even number. If None is given, iterate until convergence.
rtolfloat, optional: Relative tolerance parameter (see Notes).
atolfloat, optional: Absolute tolerance parameter (see Notes).
callbackcallable, optional: Function called with the current iterate in each iteration.

Returns

est_opnormfloat: The estimated operator norm of op.

Notes

The operator norm $||A||$ is defined by as the smallest number such that

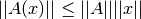
$||A(x)|| \leq ||A|| ||x||$

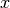for all $x$ in the domain of $A$ .

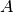The operator is evaluated until maxiter operator calls or until the relative error is small enough. The error measure is given by

abs(a - b) <= (atol + rtol * abs(b)),

where a and b are consecutive iterates.

Examples

Verify that the identity operator has norm close to 1:

>>> space = odl.uniform_discr(0, 1, 5)
>>> id = odl.IdentityOperator(space)
>>> estimation = power_method_opnorm(id)
>>> round(estimation, ndigits=3)
1.0