NormOperator.derivative

NormOperator.derivative(self, point)[source]

Derivative of this operator in point.

NormOperator().derivative(y)(x) == (y / y.norm()).inner(x)

This is only applicable in inner product spaces.

Parameters
pointdomain element-like

Point in which to take the derivative.

Returns
derivativeInnerProductOperator
Raises
ValueError

If point.norm() == 0, in which case the derivative is not well defined in the Frechet sense.

Notes

The derivative cannot be written in a general sense except in Hilbert spaces, in which case it is given by

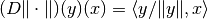
(D \|\cdot\|)(y)(x) = \langle y / \|y\|, x \rangle

Examples

>>> r3 = odl.rn(3)
>>> op = NormOperator(r3)
>>> derivative = op.derivative([1, 0, 0])
>>> derivative([1, 0, 0])
1.0