RectGrid

class odl.discr.grid.RectGrid(*coord_vectors)

Bases: Set

An n-dimensional rectilinear grid.

A rectilinear grid is the set of points defined by all possible combination of coordinates taken from fixed coordinate vectors.

The storage need for a rectilinear grid is only the sum of the lengths of the coordinate vectors, while the total number of points is the product of these lengths. This class makes use of that sparse storage scheme.

See Notes for details.

Attributes:

coord_vectors

Coordinate vectors of the grid.

examples

Generator creating name-value pairs of set elements.

extent

Return the edge lengths of this grid's minimal bounding box.

is_uniform

True if this grid is uniform in all axes, else False.

is_uniform_byaxis

Boolean tuple showing uniformity of this grid per axis.

max_pt

Vector containing the maximal grid coordinates per axis.

meshgrid

A grid suitable for function evaluation.

mid_pt

Midpoint of the grid, not necessarily a grid point.

min_pt

Vector containing the minimal grid coordinates per axis.

ndim

Number of dimensions of the grid.

nondegen_byaxis

Boolean array with True entries for non-degenerate axes.

shape

Number of grid points per axis.

size

Total number of grid points.

stride

Step per axis between neighboring points of a uniform grid.

Methods

append(*grids)	Insert grids at the end as a block.
approx_contains(other, atol)	Test if other belongs to this grid up to a tolerance.
approx_equals(other, atol)	Test if this grid is equal to another grid.
contains_all(other)	Test if all elements in other are contained in this set.
contains_set(other)	Test if other is a subset of this set.
convex_hull()	Return the smallest IntervalProd containing this grid.
corner_grid()	Return a grid with only the corner points.
corners([order])	Corner points of the grid in a single array.
element()	An arbitrary element, the minimum coordinates.
insert(index, *grids)	Return a copy with grids inserted before index.
is_subgrid(other[, atol])	Return True if this grid is a subgrid of other.
max(**kwargs)	Return max_pt.
min(**kwargs)	Return min_pt.
points([order])	All grid points in a single array.
squeeze([axis])	Return the grid with removed degenerate (length 1) dimensions.

__init__(*coord_vectors)

Initialize a new instance.

Parameters:

vec1,...,vecNarray-like

The coordinate vectors defining the grid points. They must be sorted in ascending order and may not contain duplicates. Empty vectors are not allowed.

Notes

In 2 dimensions, for example, given two coordinate vectors

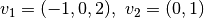
the corresponding rectilinear grid 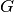is the set of all 2d points whose first component is from 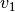and the second component from :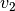

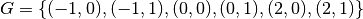
Here is a graphical representation:

   :    :        :
   :    :        :
1 -x----x--------x-...
   |    |        |
0 -x----x--------x-...
   |    |        |
  -1    0        2

Apparently, this structure can represent grids with arbitrary step sizes in each axis.

Note that the above ordering of points is the standard 'C' ordering where the first axis (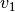) varies slowest. Ordering is only relevant when the point array is actually created; the grid itself is independent of this ordering.

Examples

>>> g = RectGrid([1, 2, 5], [-2, 1.5, 2])
>>> g
RectGrid(
    [ 1.,  2.,  5.],
    [-2. ,  1.5,  2. ]
)
>>> g.ndim  # number of axes
2
>>> g.shape  # points per axis
(3, 3)
>>> g.size  # total number of points
9

Grid points can be extracted with index notation (NOTE: This is slow, do not loop over the grid using indices!):

>>> g = RectGrid([-1, 0, 3], [2, 4, 5], [5], [2, 4, 7])
>>> g[0, 0, 0, 0]
array([-1.,  2.,  5.,  2.])

Slices and ellipsis are also supported:

>>> g[:, 0, 0, 0]
RectGrid(
    [-1.,  0.,  3.],
    [ 2.],
    [ 5.],
    [ 2.]
)
>>> g[0, ..., 1:]
RectGrid(
    [-1.],
    [ 2.,  4.,  5.],
    [ 5.],
    [ 4.,  7.]
)