Discretizations¶
Mathematical background¶
In mathematics, the term discretization stands for the transition from abstract, continuous,
often infinite-dimensional objects to concrete, discrete, finite-dimensional counterparts. We define
discretizations as tuples encompassing all necessary aspects involved in this transition. Let
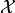 be an arbitrary set,
be an arbitrary set, 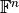 be the set of
be the set of 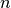 -tuples where
each component lies in
-tuples where
each component lies in 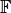 . We define two mappings
. We define two mappings
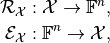
which we call sampling and interpolation, respectively. Then, the discretization of
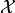 with respect to
with respect to 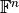 and the above operators is defined as the
tuple
and the above operators is defined as the
tuple
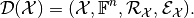
The following abstract diagram visualizes a discretization:
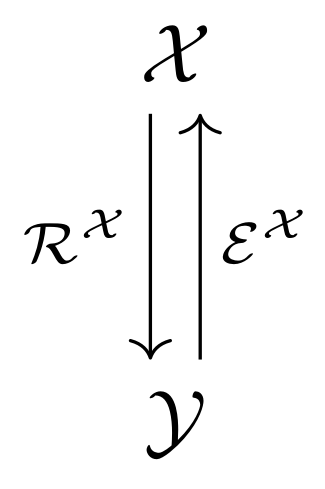
TODO: write up in more detail
Example¶
Let ![\mathcal{X} = C([0, 1])](../_images/math/14bf5d6c49212ecfa4c3ad1b0a4f256ce2388486.png) be the space of real-valued
continuous functions on the interval
be the space of real-valued
continuous functions on the interval ![[0, 1]](../_images/math/8027137b3073a7f5ca4e45ba2d030dcff154eca4.png) , and let
, and let  be ordered sampling points in
be ordered sampling points in ![[0, 1]](../_images/math/8027137b3073a7f5ca4e45ba2d030dcff154eca4.png) .
.
Restriction operator:
We define the grid collocation operator as
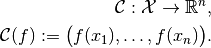
The abstract object in this case is the input function 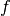 , and
the operator evaluates this function at the given points, resulting in
a vector in
, and
the operator evaluates this function at the given points, resulting in
a vector in 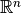 .
.
This operator is implemented as PointCollocation.
Extension operator:
Let discrete values 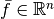 be given. Consider the linear interpolation
of those values at a point
be given. Consider the linear interpolation
of those values at a point ![x \in [0, 1]](../_images/math/430e3f359414ead5985175435ae8bc3dc9a019f0.png) :
:
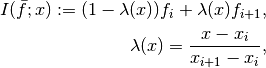
where 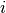 is the index such that
is the index such that 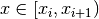 .
.
Then we can define the linear interpolation operator as
![\mathcal{L} : \mathbb{R}^n \to C([0, 1]),
\mathcal{L}(\bar f) := I(\bar f; \cdot),](../_images/math/e910a25f1ef6493b9d4dacbaa0503aef3785ee3a.png)
where 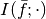 stands for the function
stands for the function
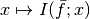 .
.
Hence, this operator maps the finite array 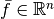 to the abstract interpolating function
to the abstract interpolating function 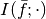 .
.
This interpolation scheme is implemented in the LinearInterpolation operator.