parallel_beam_geometry¶

odl.tomo.geometry.parallel.parallel_beam_geometry(space, num_angles=None, det_shape=None)[source]¶

Create default parallel beam geometry from space.

This is intended for simple test cases where users do not need the full flexibility of the geometries, but simply want a geometry that works.

This default geometry gives a fully sampled sinogram according to the Nyquist criterion, which in general results in a very large number of samples. In particular, a space that is not centered at the origin can result in very large detectors.

Parameters:

spaceDiscretizedSpace: Reconstruction space, the space of the volumetric data to be projected. Needs to be 2d or 3d.
num_anglesint, optional: Number of angles. Default: Enough to fully sample the data, see Notes.
det_shapeint or sequence of int, optional: Number of detector pixels. Default: Enough to fully sample the data, see Notes.

Returns:

geometryParallelBeamGeometry: If space is 2d, return a Parallel2dGeometry. If space is 3d, return a Parallel3dAxisGeometry.

Notes

According to [NW2001], pages 72--74, a function 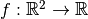$f : \mathbb{R}^2 \to \mathbb{R}$ that has compact support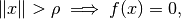

$\| x \| > \rho \implies f(x) = 0,$

and is essentially bandlimited

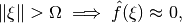
$\| \xi \| > \Omega \implies \hat{f}(\xi) \approx 0,$

can be fully reconstructed from a parallel beam ray transform if (1) the projection angles are sampled with a spacing of 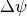$\Delta \psi$ such that

$\Delta \psi \leq \frac{\pi}{\rho \Omega},$

and (2) the detector is sampled with an interval $\Delta s$ that satisfies

$\Delta s \leq \frac{\pi}{\Omega}.$

The geometry returned by this function satisfies these conditions exactly.

If the domain is 3-dimensional, the geometry is "separable", in that each slice along the z-dimension of the data is treated as independed 2d data.

References

[NW2001]

Natterer, F and Wuebbeling, F. Mathematical Methods in Image Reconstruction. SIAM, 2001. https://dx.doi.org/10.1137/1.9780898718324

Examples

Create a parallel beam geometry from a 2d space:

>>> space = odl.uniform_discr([-1, -1], [1, 1], (20, 20))
>>> geometry = parallel_beam_geometry(space)
>>> geometry.angles.size
45
>>> geometry.detector.size
31