NumpyTensorSpace¶

class odl.space.npy_tensors.NumpyTensorSpace(shape, dtype=None, **kwargs)[source]¶

Bases: TensorSpace

Set of tensors of arbitrary data type, implemented with NumPy.

A tensor is, in the most general sense, a multi-dimensional array that allows operations per entry (keep the rank constant), reductions / contractions (reduce the rank) and broadcasting (raises the rank). For non-numeric data type like object, the range of valid operations is rather limited since such a set of tensors does not define a vector space. Any numeric data type, on the other hand, is considered valid for a tensor space, although certain operations - like division with integer dtype - are not guaranteed to yield reasonable results.

Under these restrictions, all basic vector space operations are supported by this class, along with reductions based on arithmetic or comparison, and element-wise mathematical functions ("ufuncs").

This class is implemented using numpy.ndarray's as back-end.

See the Wikipedia article on tensors for further details. See also [Hac2012] "Part I Algebraic Tensors" for a rigorous treatment of tensors with a definition close to this one.

Note also that this notion of tensors is the same as in popular Deep Learning frameworks.

References

[Hac2012] Hackbusch, W. Tensor Spaces and Numerical Tensor Calculus. Springer, 2012.

Attributes:

byaxis: Return the subspace defined along one or several dimensions.
complex_dtype: The complex dtype corresponding to this space's dtype.
complex_space: The space corresponding to this space's complex_dtype.
default_order: Default storage order for new elements in this space: 'C'.
dtype: Scalar data type of each entry in an element of this space.
element_type: Type of elements in this space: NumpyTensor.
examples: Return example random vectors.
exponent: Exponent of the norm and the distance.
field: Scalar field of numbers for this vector space.
impl: Name of the implementation back-end: 'numpy'.
is_complex: True if this is a space of complex tensors.
is_real: True if this is a space of real tensors.
is_weighted: Return True if the space is not weighted by constant 1.0.
itemsize: Size in bytes of one entry in an element of this space.
nbytes: Total number of bytes in memory used by an element of this space.
ndim: Number of axes (=dimensions) of this space, also called "rank".
real_dtype: The real dtype corresponding to this space's dtype.
real_space: The space corresponding to this space's real_dtype.
shape: Number of scalar elements per axis.
size: Total number of entries in an element of this space.
weighting: This space's weighting scheme.

Methods

`astype`(dtype)	Return a copy of this space with new `dtype`.
`available_dtypes`()	Return the set of data types available in this implementation.
`contains_all`(other)	Test if all elements in `other` are contained in this set.
`contains_set`(other)	Test if `other` is a subset of this set.
`default_dtype`([field])	Return the default data type of this class for a given field.
`dist`(x1, x2)	Return the distance between `x1` and `x2`.
`divide`(x1, x2[, out])	Return the pointwise quotient of `x1` and `x2`
`element`([inp, data_ptr, order])	Create a new element.
`inner`(x1, x2)	Return the inner product of `x1` and `x2`.
`lincomb`(a, x1[, b, x2, out])	Implement `out[:] = a * x1 + b * x2`.
`multiply`(x1, x2[, out])	Return the pointwise product of `x1` and `x2`.
`norm`(x)	Return the norm of `x`.
`one`()	Return a tensor of all ones.
`zero`()	Return a tensor of all zeros.

__init__(shape, dtype=None, **kwargs)[source]¶

Initialize a new instance.

Parameters:

shapepositive int or sequence of positive ints

Number of entries per axis for elements in this space. A single integer results in a space with rank 1, i.e., 1 axis.

dtype

Data type of each element. Can be provided in any way the numpy.dtype function understands, e.g. as built-in type or as a string. For None, the default_dtype of this space (float64) is used.

exponentpositive float, optional

Exponent of the norm. For values other than 2.0, no inner product is defined.

This option has no impact if either dist, norm or inner is given, or if dtype is non-numeric.

Default: 2.0

Other Parameters:

weightingoptional

Use weighted inner product, norm, and dist. The following types are supported as weighting:

None: no weighting, i.e. weighting with 1.0 (default).

Weighting: Use this weighting as-is. Compatibility with this space's elements is not checked during init.

float: Weighting by a constant.

array-like: Pointwise weighting by an array.

This option cannot be combined with dist, norm or inner. It also cannot be used in case of non-numeric dtype.

distcallable, optional

Distance function defining a metric on the space. It must accept two NumpyTensor arguments and return a non-negative real number. See Notes for mathematical requirements.

By default, dist(x, y) is calculated as norm(x - y).

This option cannot be combined with weight, norm or inner. It also cannot be used in case of non-numeric dtype.

normcallable, optional

The norm implementation. It must accept a NumpyTensor argument, return a non-negative real number. See Notes for mathematical requirements.

By default, norm(x) is calculated as inner(x, x).

This option cannot be combined with weight, dist or inner. It also cannot be used in case of non-numeric dtype.

innercallable, optional

The inner product implementation. It must accept two NumpyTensor arguments and return an element of the field of the space (usually real or complex number). See Notes for mathematical requirements.

This option cannot be combined with weight, dist or norm. It also cannot be used in case of non-numeric dtype.

kwargs

Further keyword arguments are passed to the weighting classes.

See also

odl.space.space_utils.rn: constructor for real tensor spaces
odl.space.space_utils.cn: constructor for complex tensor spaces
odl.space.space_utils.tensor_space: constructor for tensor spaces of arbitrary scalar data type

Notes

A distance function or metric on a space 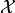$\mathcal{X}$ is a mapping $d:\mathcal{X} \times \mathcal{X} \to \mathbb{R}$ satisfying the following conditions for all space elements $x, y, z$ :
- $d(x, y) \geq 0$ ,
- $d(x, y) = 0 \Leftrightarrow x = y$ ,
- $d(x, y) = d(y, x)$ ,
- $d(x, y) \leq d(x, z) + d(z, y)$ .
A norm on a space 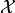$\mathcal{X}$ is a mapping $\| \cdot \|:\mathcal{X} \to \mathbb{R}$ satisfying the following conditions for all space elements $x, y$ : and scalars $s$ :
- $\| x\| \geq 0$ ,
- $\| x\| = 0 \Leftrightarrow x = 0$ ,
- $\| sx\| = |s| \cdot \| x \|$ ,
- $\| x+y\| \leq \| x\| + \| y\|$ .
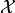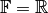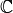An inner product on a space $\mathcal{X}$ over a field $\mathbb{F} = \mathbb{R}$ or $\mathbb{C}$ is a mapping $\langle\cdot, \cdot\rangle: \mathcal{X} \times \mathcal{X} \to \mathbb{F}$ satisfying the following conditions for all space elements $x, y, z$ : and scalars $s$ :
- $\langle x, y\rangle = \overline{\langle y, x\rangle}$ ,
- $\langle sx + y, z\rangle = s \langle x, z\rangle + \langle y, z\rangle$ ,
- $\langle x, x\rangle = 0 \Leftrightarrow x = 0$ .

Examples

Explicit initialization with the class constructor:

>>> space = NumpyTensorSpace(3, float)
>>> space
rn(3)
>>> space.shape
(3,)
>>> space.dtype
dtype('float64')

A more convenient way is to use factory functions:

>>> space = odl.rn(3, weighting=[1, 2, 3])
>>> space
rn(3, weighting=[1, 2, 3])
>>> space = odl.tensor_space((2, 3), dtype=int)
>>> space
tensor_space((2, 3), dtype=int)