proximal_convex_conj_kl¶
- odl.solvers.nonsmooth.proximal_operators.proximal_convex_conj_kl(space, lam=1, g=None)[source]¶
Proximal operator factory of the convex conjugate of the KL divergence.
Function returning the proximal operator of the convex conjugate of the functional F where F is the entropy-type Kullback-Leibler (KL) divergence:
F(x) = sum_i (x_i - g_i + g_i ln(g_i) - g_i ln(pos(x_i))) + ind_P(x)
with
xandgelements in the linear spaceX, andgnon-negative. Here,posdenotes the nonnegative part, andind_Pis the indicator function for nonnegativity.- Parameters:
- space
TensorSpace Space X which is the domain of the functional F
- lampositive float, optional
Scaling factor.
- g
spaceelement, optional Data term, positive. If None it is take as the one-element.
- space
- Returns:
- prox_factoryfunction
Factory for the proximal operator to be initialized.
See also
proximal_convex_conj_kl_cross_entropyproximal for releated functional
Notes
The functional is given by the expression

The indicator function
 is used to restrict the
domain of
is used to restrict the
domain of 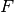 such that
such that 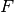 is defined over whole space
is defined over whole space
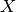 . The non-negativity thresholding
. The non-negativity thresholding  is used to define
is used to define
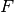 in the real numbers.
in the real numbers.Note that the functional is not well-defined without a prior g. Hence, if g is omitted this will be interpreted as if g is equal to the one-element.
The convex conjugate
 of
of 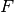 is
is
where
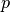 is the variable dual to
is the variable dual to 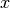 , and
, and  is an
element of the space
is an
element of the space 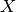 with all components set to 1.
with all components set to 1.The proximal operator of the convex conjugate of F is

where
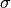 is the step size-like parameter, and
is the step size-like parameter, and 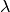 is the weighting in front of the function
is the weighting in front of the function 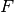 .
.KL based objectives are common in MLEM optimization problems and are often used when data noise governed by a multivariate Poisson probability distribution is significant.
The intermediate image estimates can have negative values even though the converged solution will be non-negative. Non-negative intermediate image estimates can be enforced by adding an indicator function ind_P the primal objective.
This functional
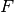 , described above, is related to the
Kullback-Leibler cross entropy functional. The KL cross entropy is the one
described in this Wikipedia article, and
the functional
, described above, is related to the
Kullback-Leibler cross entropy functional. The KL cross entropy is the one
described in this Wikipedia article, and
the functional 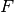 is obtained by switching place of the prior and
the varialbe in the KL cross entropy functional. See the See Also section.
is obtained by switching place of the prior and
the varialbe in the KL cross entropy functional. See the See Also section.